Verne Világfelfordulás című regényében a holdutazásukkal nevezetessé vált Gun Club tagjai új, dörgedelmes szenzációra készülnek. A Föld köztudomásúan ferde, a keringés síkjával 66,5°-os szöget bezáró tengelyét akarják merőlegesre állítani, mégpedig klubjuk nevéhez (gun = ágyú) és hagyományaihoz hűen, egy óriási ágyúlövés reakcióerejével.
Kísérletük a rosszul megválasztott méretek miatt kudarcot vall: a löveg nem tud elég nagy lökést adni glóbuszunknak. Ezzel az évszázad üzlete esik kútba – de nem akarjuk az egész történetet elmesélni.
Az alapötletnél a derék baltimore-i tüzérek egyebek között arról is megfeledkeztek, hogy egy ilyen beavatkozásra bolygónk ún. precessziós mozgása is megélénkülne, és óriási búgócsiga módjára, hatalmasan hajbókolva folytatná Nap körüli keringését. E szabálytalan (pontosabban igen bonyolult szabályokat követő) mozgás eredményeként a napok hossza alaposan megváltozna, sőt a Nap kelésének és nyugvásának irányai sem lennének a szokásosak. Mindkét féltekén beláthatatlan időjárási zavarokat okozna a napsütés mennyiségének ingadozása; szökőárak és pusztító szárazságok sújtanák bolygónk valamennyi vidékét.
Szolgáljon a tévedők mentségére, hogy a klasszikus fizika egyik legbonyolultabb jelenségét, a pörgettyűhatást hagyták figyelmen kívül. E spontán szemlélettel a legkevésbé sem nyilvánvaló kérdéskör összetettségét már a vonatkozó szakirodalom mennyisége is jellemzi. Szinte hihetetlen, hogy a köztudatban afféle együgyű játékszerként ismert eszközről több kötetes, vaskos szakkönyvek születtek. A magyar nyelvű szakirodalom egyetemi tankönyveink néhány fejezetére korlátozódik.
A pörgettyűmozgás differenciálegyenleteit már Euler felállította. Az elmúlt két évszázadban sok tudós foglalkozott megoldásukkal, a legáltalánosabb mozgások leírására azonban csak napjaink számítógépi módszerei adtak lehetőséget.
Számos természeti jelenség, műszaki probléma vagy éppen konstrukciós ötlet alapja a pörgettyű. A bolygók mozgásától az atomfizikáig, a navigációtól a diszkoszvetésig sok helyen bukkanunk hatásaira.
Tekintsük át a leggyakoribb, szimmetrikus pörgettyű néhány jellegzetességét!
Az erőmentes pörgettyű
A 18. század derekán a magyar Segner, majd tőle függetlenül Euler is felfedezte, hogy bármely merev testhez kijelölhető három, a súlyponton átmenő és egymásra kölcsönösen merőleges ún. főtengelyirány. Ezek valamelyike körül a test állandó szögsebességű forgását külső energia nélkül képes fenntartani – természetesen elhanyagolva a fékező (pl. súrlódási, légellenállási stb.) hatásokat.
A forgástestek szimmetriatengelyei mindig ilyen tulajdonságúak. Az általuk kijelölt $1, 2, 3$ főtehetetlenségi irányokhoz a $J_1, J_2, J_3$ főtehetetlenségi nyomatékok tartoznak. (Ezek az egyes tengelyek körül a testet forgatni akaró nyomatékokkal szembeni ellenállások, a „forgási tehetetlenség” mérőszámai.)
Stabil forgási állapot a legnagyobb főtehetetlenségi nyomatékhoz tartozó tengely körül jön létre, ezt szemléltetik az 1–2. ábrák. (A függesztőzsinór íves alakja jól demonstrálja azt a tényt, hogy a forgó testeket nem a felfüggesztés tartja vízszintesen.)
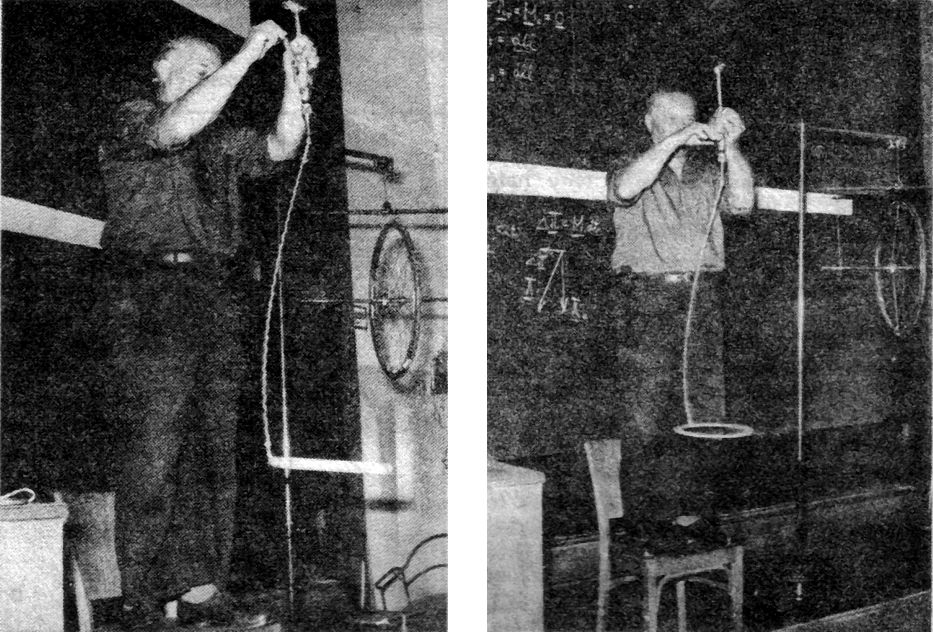
A mozgásállapotot a test perdületvektora és mozgási energiájának mennyisége jellemzi. A perdületvektort általában a súlypontból induló irányított vonaldarabbal szemléltetik, mely csak akkor változik meg, ha a testre külső nyomaték hat.
Amennyiben a test a súlypontján átmenő, általános állású tengely körül forog, perdületvektora a testtel együtt mozgó koordináta-rendszerben (melynek tengelyei a főirányokba mutatnak):
ahol $\omega_{1}$, $\omega_{2}$, $\omega_{3}$ az $\omega$ szögsebességvektor koordinátái.
A mozgási energia ekkor
Egy merev testet akkor nevezünk pörgettyűnek, ha mozgása közben valamely pontja nyugalomban marad.
Az erőmentes pörgettyű úgy van rögzítve, hogy éppen súlypontja őrzi meg a helyzetét (2. ábra).

Ha a pörgettyűt pl. az 1. főtengelye körül $\omega$ szögsebességre gyorsítjuk, a forgástengely, a perdület és szögsebesség vektorai egyazon egyenest jelölik ki. Ebből a helyzetből egy kis lökéssel kitérítve a további mozgást két alapvető tény határozza meg:
- Mivel a lökés után külső hatás már nem ébred (vagy attól eltekintünk), a pörgettyű mozgási energiája nem változik.
- Külső nyomaték híján a perdület sem változik, vagyis vektora térben és időben állandó lesz.
Ha az (1) egyenletet skalárisan (az egyes vektorösszetevőket külön-külön) megszorozzuk az $\omega$ vektor összetevőivel, majd a szorzatkomponensek összegét felezzük, a mozgási energia (2) kifejezéséhez jutunk:
Két vektor skalárszorzata abszolút értékeik és bezárt $\phi$ szögük cosinusának szorzatával egyenlő, azaz
A (2.) és 14.1 egyenletek egyszerű átalakításával az
Illetve a
kifejezésekhez jutunk.
Az erőmentes pörgettyű forgástengelye, perdület- és szögsebességvektorai a lökés után már nem esnek egy egyenesbe. Az (5) egyenlet matematikai tartalma szerint a szögsebességvektor végpontja mindenkor egy ellipszoidfelületen van.
Mivel a $\pi$ perdület és az $E$ mozgási energia változatlanok, a (6) kifejezés szerint $\omega$-nak a perdületvektorra eső merőleges vetülete is állandó hosszúságú. Ekkor azonban a szögsebességvektor végpontja a perdületre merőleges, állandó helyzetű ún. invariábilis síkon is rajta van.
Az ellipszoid a pörgettyűvel együtt mozgó felületként képzelendő el. A nutációnak nevezett jelenség során az ellipszoid a képzeletbeli invariábilis síkon gördül, míg a pörgettyű tengelye a nutációs kúp palástját írja le (3. ábra).
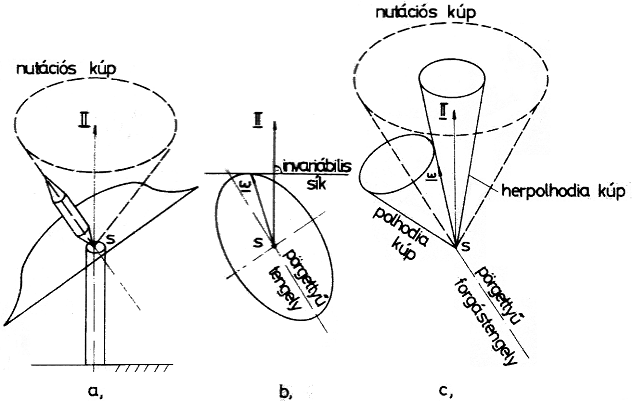
A szögsebesség- és perdületvektor, valamint a pörgettyű szimmetriatengelye mindig közös síkban fekszenek.
A szögsebességvektor ugyancsak egy kúppalást mentén mozog, mely felület az ún. herpolhodiakúp.
A nutációs és herpolhodiakúpok közös tengelye a perdületvektor. A nutációt úgy is elképzelhetjük, hogy mozgás közben a herpolhodiakúpon egy további, ún. polhodiakúp gördül. A két kúp közös alkotója a szögsebességvektor, melynek végpontja az invariábilis síkra „támaszkodik”.
A keringő polhodiakúp tengelye a nutációs kúp palástját súrolja, míg a polhodiakúp tengelye a pörgettyű szimmetriatengelye.
A súlyos pörgettyű
Ha a forgástestet súlypontján kívül rögzítjük, súlyos pörgettyűhöz jutunk. Ilyet szemléltet a 4. ábra: a pörgettyű tengelyének csúcsa az asztalon áll, míg szimmetriatengelye egy kúpfelület mentén kering.

Tapasztalat szerint a kellő fordulatszámra felgyorsított pörgettyű szimmetriatengelye vagy függőlegesen áll, vagy az ábra szerinti mozgást végzi.
Általánosan a súlyos pörgettyű a forgástengelye és a kitérítő hatás által meghatározott síkra merőlegesen igyekszik kitérni.
E jelenség mechanikai értelmezéséhez az az alaptétel ad segítséget, mely szerint a perdület idő szerinti megváltozása a testre ható külső (esetünkben a súlyerőből származó) nyomatékkal egyenlő. Az elemi kis $dt$ idő alatt a perdület $d\pi$-vel változik. A nyomaték vektora
A kezdeti $\pi$ perdület $dt$ idő múlva
értékre módosul. Esetünkben a forgást nem gyorsítja a saját súly hatása, csupán a perdület irányát változtatja meg. Az irányváltozást az
precessziós szögsebesség jellemzi (5. ábra).
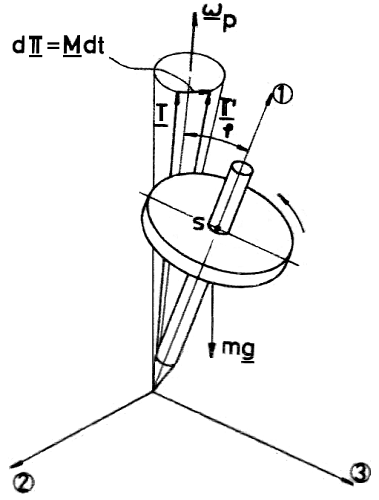
Mivel a perdületvektor nagysága állandó, a (7) egyenlet abszolút értéke bizonyíthatóan
Az általános külső erő hatására válaszként létrejövő pörgettyűnyomaték igen nagy lehet. Kiküszöbölése vagy éppen hasznosítása a pörgettyűs szerkezetek legalapvetőbb kérdése; demonstrálása igen látványos kísérletekkel történik (6–7. ábrák).


A bemutatott jelenségek csak töredékét képezik a teljes problémakörnek. A pörgettyű mozgásai a klasszikus mechanikán túl napjaink izgalmas, még születőben levő diszciplínájában, a katasztrófaelméletben is felvetődnek.
A stabil és labilis állapotok egy igen érdekes összefüggését jeleníti meg a 8–9. ábrán látható szerkezet. Az aszimmetrikus kardánfelfüggesztésű pörgettyűnek két labilis nyugalmi helyzete van. A 2. keretet az A–A tengely körül elforgatva a legfelső állásban labilis egyensúlyi helyzethez jutunk. A B–B tengely körül a 3. keretet – a C rugó ellenében – a rugó maximálisan feszített helyzetéig forgatva a másik bizonytalan nyugalmi állapotot hozhatjuk létre. A legcsekélyebb külső hatásra azonban a szerkezet stabil állapotába lendül át: ilyen pedig az S súlypont legmélyebb, illetve a rugó legkevésbé feszített helyzetében van.
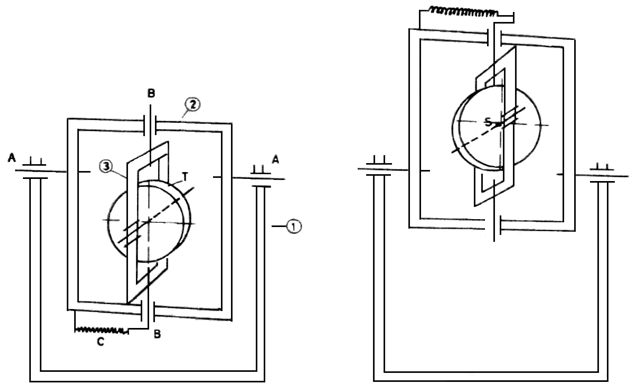

A T tárcsát felgyorsítva a két, külön-külön instabil helyzet együtt stabillá válik. Egy határfordulatszám fölött a pörgettyű minden kitérítő hatás után ide tér vissza.
Az ismertetett modellhez hasonló konstrukciókat pl. az egysínű vasutak stabilizálására használják.
Pörgettyűk a gyakorlatban
A főtehetetlenségi tengely körüli forgás stabilitását használja ki sok akrobata és zsonglőr. A légtornász- és egyensúlyozó-számok nagy részében fellelhetők az 1. ábrasoron szemléltetett törvényszerűségek.
Hajók, repülőgépek és űrobjektumok navigációjához okvetlen szükséges egy állandó viszonyítási irány ismerete. A célba találás érdekében hasonlóan fontos a mozgó hadihajók, a terepen bukdácsoló harckocsik lövegcsöveinek állandó célon tartása.
E feladatokra elterjedten használják a különféle, egyidejűleg több forgó tömeggel is dolgozó giroszkóp-mechanizmusokat. Valamennyiük működését a kényszerített precesszió biztosítja.
A pörgettyűs iránytűk, műhorizontok, dőlésmérők ismertetése a felsorolt magyar nyelvű könyvekben megtalálható. A téma iránt érdeklődő olvasónak javasoljuk még Walter Conrad A Jákob-pálcától a műholdas navigációig című kötetét (Gondolat zsebkönyvek, 1982).
A pörgettyű egy igen érdekes haditechnikai alkalmazása valósult meg a II. világháborús V–2 szárnyas rakétában.
A rakéta hajtóműve indítás után mindössze egy percig üzemelt, ezalatt gyorsította fel és állította pályára a robbanótestet, mely azután már a ferde hajítás törvényei szerint haladt tovább.
A mindenkori gyorsulásállapotnak optimálisan megfelelő tüzelőanyag-adagolásra készült a 10. ábrán (erősen egyszerűsítve) vázolt szerkezet.
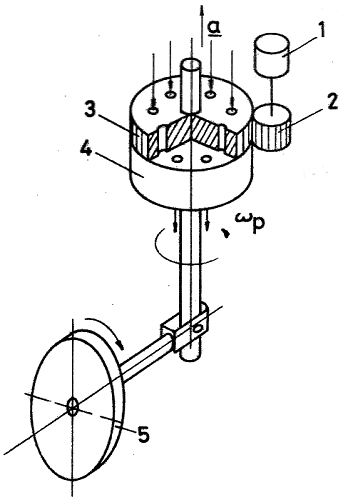
Az 1. szinkronmotor rádiójellel vezérelve állandó fordulatszámmal hajtotta a 3. jelű tárcsát. E tárcsa furataira felülről vezették a tüzelőanyagot.
A 3-assal egytengelyű, de tőle független, azonos furatosztással ellátott 4 tárcsát egy 5. jelű, nagy (kb. 30 000/perc) fordulatszámú, precesszióra kényszerített pörgettyű forgatta.
A mechanikai jellemzőket úgy hangolták össze, hogy a tárcsák a rakéta a gyorsulásvektorának megfelelően vagy együtt forogtak, vagy pedig – a különböző fordulatszámok miatt – a furatok csak időnként találkoztak. A nyílások együttállásakor a tüzelőanyag azokon át tudott áramlani, egyébként nem. Az $a$ gyorsulás növekedésével az $\omega_\rho$ precessziós szögsebesség is növekedett, tehát a rakéta „megugrásakor” a furatokon kevés tüzelőanyag ment át. Lassuláskor az $\omega_\rho$ csökkent, a két tárcsa mindinkább együtt forgott, a furatokon keresztül sok üzemanyag jutott a hajtóműbe, a rakéta tehát gyorsult.
A célirányosan előállított jelenségekkel szemben a pörgettyűhatás kellemetlen is lehet. Például a Kandó-mozdonyban az egyfázisú váltóáramot háromfázisúvá alakító hatalmas forgógép a jármű kisiklását okozhatta volna, ha zseniális tervezője előre nem gondoskodik a pörgettyűnyomaték hatástalanításáról. A több tonnás generátor megfelelő felfüggesztésével és elfordulásának biztosításával a probléma már a rajztáblán megoldódott.
A légcsavaros repülőgépek propellerjei mint óriást pörgettyűk ugyancsak megnehezítik az irányváltoztatást; több szárnytörésből fakadó katasztrófát okozott már a hirtelen fellépő pörgettyűnyomaték. Az egymotoros gép jobb vagy bal fordulójában orr- vagy faroknehéz helyzet jön létre, ennek megszüntetése a magassági kormány manővereivel lehetséges.
Az űrhajók kabinrészeinek jellegzetesen zömök alakját az a megfontolás szolgáltatja, hogy az ilyen formájú testek a hossztengelyük körül forogva stabil helyzetűek. Éppígy a jól eldobott diszkosz vagy a lövegcsőben a huzagolással felpörgetett lövedék a légellenállás leküzdéséhez a legkedvezőbb helyzetben repül. Külső zavar (pl. széllökés) hatására olyan pörgettyűnyomaték ébred rajtuk, amely nem engedi meg a kitérés növekedését, sőt éppen csökkenti azt.
Az ember készítette tárgyak mellett az anyag szubatomi részecskéire is érvényesek a pörgettyűmozgás törvényei.
A hidrogén atommagja, a proton forgó elemi mágnesként fogható fel. Mágneses erőtérben az erővonalakkal párhuzamosan forgása (spinje) miatt nem tud beállni, hanem a térirány körül meghatározott frekvenciával precessziót végez.
A proton a mágneses térben átfordulhat, ha energiaszintje megváltozik. Erre akkor nyílik lehetőség, ha az elektromágneses sugárzás frekvenciája megegyezik az „elemi” mágnes precessziós frekvenciájával. A rezonanciahelyzetben a proton átbillen, de közben jellegzetes mennyiségű energiát nyel el. Az energia felvétel alapján számos következtetés vonható le az anyag mikroszerkezetéről. (Ezt a vizsgálati elvet használja fel az atommagok tanulmányozására kifejlesztett magrezonancia-elemző készülék.)
A Föld mint pörgettyű
Bolygónk egyenlítője mentén az elméleti gömbalaktól eltérő, kb. 20 km magas, övszerű kidudorodás található. (A gravitációs térerő és a centrifugális erő vektori eredőjének következménye ez a bolygó méreteihez képest kicsiny, de figyelmen kívül semmiképpen sem hagyható torzulás.)
Mivel a Föld forgási és keringési síkjai 23,5°-os szöget zárnak be, a Napnak az egyenlítői övre gyakorolt vonzása forgatónyomatékot eredményez. E nyomaték a Föld tengelyét merőleges irányba akarja beállítani – éppúgy, ahogy azt Barbicane és Maston, a Gun Club vezetői szerették volna.
Az állandó külső hatás következtében bolygónk precessziós mozgásra kényszerül úgy, hogy a forgástengelye a 23,5°-os fél nyílásszögű kúp mentén 25 800 évenként egyszer körbefordul. Ebből az ún. szoláris precesszióból származik a tavaszpont vándorlása, a jégkorszakok ismétlődése.
A Hold pályasíkja a Földével 5’-os szöget zár be. A többi bolygó hatása a Hold forgástengelyét kényszeríti 18,6 éves periódusidejű precesszióra – ez azonban befolyásolja a Föld–Hold kölcsönhatást is. A szoláris precesszióhoz a 11. ábrán hullámos vonallal jelzett pályaháborgással járul égi kísérőnk. E két hatás együttese az ún. luniszoláris precesszió.
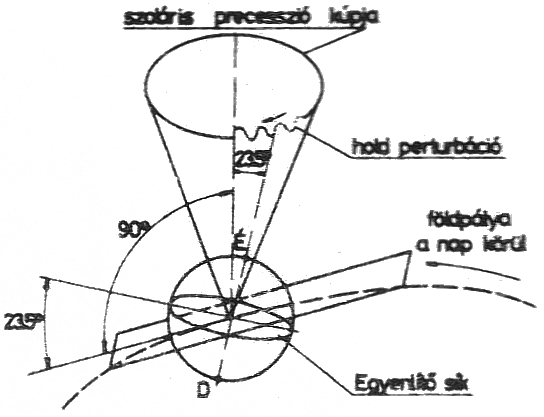
Még csekélyebb, de ugyancsak kimutatható mértékben növeli a földtengely billegését a naprendszerbeli bolygók vonzása. Emiatt – az ún. planetáris precesszió eredményeként – a Föld forgástengelye kb. 40 000 éves periódusidővel egy további, 1,5° fél nyílásszögű kúpot is leír.
Látható tehát, hogy a pörgettyűhatás egyáltalán nem jelentéktelen mechanikai hatás. A búgócsiga viselkedését befolyásoló törvények az egyre nagyobb fordulatszámon dolgozó golyóscsapágyak élettartamát éppúgy módosíthatják, mint ahogy bolygónk éghajlatának változásával az egész emberiség hosszabb távú jövőjét.
(E cikk a Természet Világa 1982. évi pályázatán dicséretben részesült.)
A fényképeket Németh Ernő készítette dr. Ludvig Győzőnek a Budapesti Műszaki Egyetemen tartott előadásán.