„Már Copernicus és Kepler sejtették az általános gravitációt; Boullian és Borelli pedig határozottan úgy tartották, hogy lennie kell egy, a három Kepler-törvényt összefogó elvnek, – sőt, a zseniális Pascal – ha ugyan a Chasles által közölt kéziratok nem eleitől-végig csalás termékei – már formulába is öntötte volna, egy 1652 körül Boyle-hez írt levelében:
« Dans les mouvements célestes la force, agissant en raison directe des masses et en raison inverse du quarré de la distance, suffit à tout et fournit des raisons pour expliquer toutes ces grandes révolutions qui animent l’Univers. »
(„Az égi mozgásokban a tömeggel egyenes arányban, a távolság négyzetével fordított arányban ható erő elegendően magyarázza mindazokat a nagy fordulatokat amelyek az univerzumot életben tartják.”)
– de még akkor is hiányzott az elv bizonyítása és részletes következményeinek a kifejtése és ezt mindenképp a hasonlíthatatlan Newton végezte el először. […] Úgy tűnik, Gauss kételyei ellenére is hinni kell unokahúga, Mme Conduit és barátja, Henry Pemberton elbeszélésének, hogy mikor az 1665-ös pestisjárvány elől Newton Cambridge-ből hazaűzetvén, kedvenc szokása szerint egy fa árnyékában gondolkozott, egy leeső alma arra a kérdésre vezette, vajon ugyanaz az erő tartja-e a Holdat is Föld körüli pályáján, amelyik az almát esni kényszeríti.”2
Rudolf Wolf, a XIX. század egyik legtekintélyesebb asztronómiatörténésze kérdezte ezt Newton nevében. Azonnal válaszol: a Holdat is ugyanaz a gravitációs erő vonzza a Föld felé, mint a földön szabadon eső tárgyakat, a Hold azért nem esik a Földre, mert a vonzással éppen egyenlő centrifugális erő nem engedi. A kettő éppen egyenlő, s így a centrifugális erő méri a vonzást. Ennek a centrifugális erőnek és a harmadik Kepler-törvénynek a segítségével kiszámítja, mekkora a nehézségi gyorsulás a Földön, a Hold mozgásából számítva.
De a Hold távolságára hibás, a valóságosnál kisebb adatok állnak rendelkezésére, s így a számított nehézségi erőt a tényleges földi gyorsulás kb. 86%-ának találta csupán.
Ez elveszi a kedvét.
„Cambridge-be visszatérve ismét optikai vizsgálatokkal foglalkozott. Csak 1678-ban tért vissza mechanikai vizsgálataihoz. Hooke-nak egy matematikai fejtegetése, mely a mozgó földön eső test pályájára vonatkozott, Newtont egy fontos tétel felismerésére vezette, hogy ti. a távolság négyzetével fordítva arányos erő hatása alatt álló bolygó ellipszisen mozog, melynek egyik gyújtópontjában áll a Nap. Newton ennek dacára nem gondolt rá, hogy elméletét közzé tegye, míg 1682-ben az új Picard-féle fokmérés megbízható adatairól tudomást szerzett, mire egész számítását ismételte. Most az eredmény a valóságnak elég jól megfelelt. Vizsgálatai közben még más, a bolygók keringésére vonatkozó tételeket fedezett fel. Barátjának Halley-nak unszolására Newton a maga elméletét kidolgozta, és a Royal Society-nak beküldte, mely azt 1687-ben Philosophiae naturalis principia mathematica (A természetfilozófia matematikai alapelvei. – A szerk.) cím alatt kiadta.”3
A jólértesült Wolf még azt is hozzáteszi, hogy a Principia kéziratának a Royal Society-ben való bemutatásakor
„hatte Hooke die unglaubliche Unverschämtheit, sich
zu stellen, wie wenn ihm das Meiste in den Werke Enthaltene
schon lange bekannt wäre.“4
[„Hooke még azt a hihetetlen szemtelenséget is megengedte magának, hogy azt állítsa, mindazt, ami a művekben található, már régebbről ismerte.”]
Elavult, a tudománytörténetírás „praekritikus” korszakából származó vélemények?
Nézzük meg, a második világháború utáni kor egyik legnagyobb közönségsikert elért tudománytörténete, Stephen F. Mason könyve mit tart a kérdésről. Szerinte is, Galilei és Descartes tehetetlenségi törvénye, Kepler és Borelli spekulációi után nyitva állott az út az általános gravitáció felfedezésére, s az 1660-as években az angol iskola, Robert Hooke, Christopher Wren, Edmund Halley sejtette, hogy a bolygók mozgása a távolság négyzetével fordított arányban csökkenő vonzás és a centrifugális erő kombinálásával magyarázandó.
„Ezekkel a kérdésekkel foglalkozott Newton is, amikor az 1665–66-os nagy pestis alatt Cambridge-től távol, a Grantham melletti Woolsthorpe-i birtokán tartózkodott.”
S most következik a már ismertek ismertetése
„Jóllehet Newton ezeket a számításokat Woolsthorpe-i tartózkodása alatt végezte, az eredményeit nem tette közzé. Newton 1666-os munkájának a közzé nem tételére a legkülönbözőbb magyarázatokat próbálták adni…”
Mindenesetre 1679 körül
„Waren auch andere Wissenschaftler bis zum Gesetz
für die Zentripetalkraft und zum reziprok quadratischen
Gesetz für die Gravitationskraft
vorgedrungen.“5
(„Mindenesetre 1690 körül a centripetális erő és a gravitációs erő reciprok négyzetes törvényének megismerése terén már más tudósok is elég messzire jutottak.”)
Apró javításokat nem tekintve, a leírás lényegében azonos az előzőkkel. Az „almát” kihagyta, a centrifugális erő helyett a történelmileg igazolható „Zentripetalkraft”-ot vette be és a „szemtelen” Hooke-ot az új törvény egyik előkészítőjévé léptette elő.
A „szemtelen” Hooke ugyanis azóta különös karriert futott be. A két világháború közötti kor egyik legélesebb szemű tudománytörténésze, Jean Pelseneer hívta fel a figyelmet 1929-ben egy addig kiadatlan, Hooke-hoz írt Newton-levéllel kapcsolatban, hogy Newton gravitációra vonatkozó nézetei távolról sem lehettek 1680 körül olyan fejlettek, mint az 1666-os hagyomány tartja.6 – Ez a levél egy rövid Hooke–Newton levélváltás egyik darabja, 1679. dec. 13-án írta Newton.
Hooke, aki Oldenburg halála után a Royal Society titkára lett, 1679. nov. 24-én egy kedves hangú levelet írt Newtonhoz, közreműködését kérve. És a végén saját kéréssel is fordul hozzá:
„Nagy kegynek tekinteném, ha szíveskednék kifogásait közölni bármely hipotézisemről vagy véleményemről, kiváltképpen ha megismertetné velem gondolatait a bolygók mozgásának egy egyenes, (direct) érintő irányában történő és egy központi test felé történő vonzó mozgásból való összetevésére vonatkozólag.”7
S aztán közli, hogy nagyon érdekelné az is, mi a véleménye Newtonnak Flamsteed parallaxis kísérleteiről. A kiadó itt megjegyzi, hogy Hooke évekkel azelőtt kiadott egy kis könyvet, An Attempt to Prove the Motion of the Earth from Observations (Kísérlet a megfigyelésekből a Föld mozgásának bizonyítására) (London, 1674), amelynek a végén
„Hooke nagy általánosságban leírja az univerzális gravitációt.”8
Newton meglehetősen kelletlenül válaszol 1679. nov. 28-án.9 Nagyon elfoglalt, most más kérdések érdeklik. Nem tudta, hogy Hooke-nak ilyesféle hipotézise van a gravitációra vonatkozólag, mindenesetre ehhez hasonló hipotézisek igen elterjedtek a „physical World”-ban. Mégis, hogy ne adjon teljesen kosarat, küld egy kis idevonatkozó fejtörőt. Mi lesz egy magas toronyból leejtett test pályája a földvonzás hatása alatt, feltéve, hogy az esés a föld felszíne alá is folytatódna? Azt állítja, hogy az eső test az ellenkező véleményekkel szemben nem nyugatra, hanem keletre fog eltérni, s a föld alatt egy csigavonalat leírva jut el a Föld centrumába.
Hooke 1679. dec. 9-én megköszöni, ő javít Newton állításán: a mi szélességünkön nem keletre, hanem délkeletre fog eltérni az eső test, s a pályája nem csigavonal, hanem ellipszis – lenne, legalábbis ha ellenállásmentesen mozoghatna. Így azonban az ellipszisek egyre kisebbek lesznek, s végül a test az excentrikusan elhelyezett, egyre kisebb ellipsziseken a földcentrumba zuhan.10
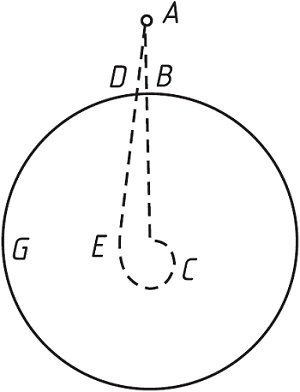

Newton már dec. 13-án válaszol: Való igaz, hogy a test a mi szélességünkön délkeletre esne, de a pálya nem olyan, mint Hooke gondolja. S ez az a levél, amit Pelseneer közölt s amiből világosan kitetszik, hogy Newton még nincs az általános tömegvonzás ismeretének birtokában. Newton beismeri, hogy első levelében tévedett: ha feltesszük, hogy a gravitás uniformis, az eső test
„nem spirálisan fog leszállani a Föld centrumába, hanem váltakozó fel- és leszállásban fog keringeni a vis centrifuga és a gravitás egymást váltakozva legyőző (alternately overballancing) hatása alatt”,
s végül is Lissajoue-görbe-szerű pályát ír le.11
Ez a levél több szempontból, nem utolsó sorban Newton matematikai módszerének a genezise szempontjából is figyelemre méltó. Most azonban csak annyit jegyzünk meg, hogy felmerül benne az a gondolat, hogy egy érintőleges mozgás és egy gravitációs vonzás hatása alatt mozgó test megkerülheti a vonzó centrumot, s a pálya, amit leír, kiszámítható. S ez óriási gondolat, mind a kettő.
Hooke-ot láthatóan nem elégíti ki a válasz. Őt más kérdés izgatja.
„Sir – írja 1679/80 jan. 6-án12 – az Ön számítása a középponttól minden távolságban egyenlő erővel vonzott test pályájára helyes, így mozog egy megfordított konkáv kúpban görgő golyó … De az én feltevésem az, hogy a vonzás mindig fordított arányban áll a távolság négyzetével, következésképpen a sebesség a vonzás négyzetgyökével lesz arányos (the Velocity will be in a subduplicate proportion to the Attraction) és következésképpen fordított arányban áll a távolsággal, amint Keppler felteszi.”
A Föld belsejében természetesen nem nő egyre jobban a centrum felé a vonzás, ellenkezőleg, csökken.
„De az égi mozgásokban a Nap, Föld, vagy központi test az oka a vonzásoknak, és bár azok nem tekinthetők matematikai pontoknak, mégis fizikai pontoknak tekinthetők és nagy távolságban a vonzásuk a fenti arány szerint mint centrumtól tőlük számítható. This Curve truly Calculated will shew the error of those many lame shifts made use of by astronomers to approach the true motions of the planets with their tables.”
A levelezés itt megszakad, Newton többé nem válaszol érdemileg. Más köti le újból a figyelmét.
A továbbiak mindenesetre már jól ismertek; Newton XIX. század közepi hagiografusa, Brewster óta számtalanszor leírták. Hogyan beszélgetnek 1684 tavaszán Hooke, Wren és a fiatal Halley a bolygómozgás törvényéről, Wren 40 shillinget érő könyvet ígér a megfejtőnek, hogyan vallja be a szerény Halley, hogy neki nem sikerült megtalálni, s hogyan henceg Hooke, hogy ő tudja; hogy megy el Halley augusztusban Newtonhoz, s hogy ad az azonnali választ, aminek a részletes igazolását később, az év végén pártfogoltjával Pagettel elküldi Halley-nak, amit 1685 elején a Royal Society regisztrál, hogyan dolgozik étlen-szomjan 18 hónapot a Principián, s az első könyv kéziratának a Royal Society-ban 1686 áprilisában történő bemutatásakor hogyan pattan fel a „szemtelen” Hooke, hogy a távolság négyzetével fordított arányban csökkenő vonzás világmindenségre való alkalmazásának a gondolatát tőle vette.
A hűséges Halley természetesen azonnal értesíti Newtont:
„Azt mondja, Ön tőle vette az ötletet, bár az így keletkező görbék bizonyítását teljesen Önének ismeri el.”13
Newton már május 27-én válaszol; rövid levélben magyarázza el Hooke-al lezajlott levélváltásának lényegét. Ő egyébként már egy évvel a Hooke-levelezés előtt beszélt a dologról Christopher Wrennel és Done-al.
„Ön ismeri Sir Christophert, Kérem, tudja meg, honnan és honnan (whence & whence) hallott először az erőnek a centrumtól számított távolság négyzetével arányos csökkenéséről.”14
Halley küldi a Principia kefelenyomatait, nem is említi Hooke-ot,15 Newton válaszában16 (1686. jún. 20) egyenesen Hooke-al kezdi. Bizonyos benne, hogy mikor 9 évvel ezelőtt meglátogatta Wrent, az már ismerte a reciprok négyzetes törvényt, Hooke viszont csak 1678-ban megjelent, üstökösökről írt könyvében közli. Így kiderül, hogy Hooke volt „az utolsó hármunk közül, aki rájött”. Ő, Newton, azonban a földi mozgások leírásában sohasem alkalmazta ezt a törvényt, és így Hooke az eső test pályájáról történt levélváltásukból nem következtethet arra, hogy nem ismerte.
Egyébként is 1673-ban, mikor megköszönte Huygens-nek a Horologium oscillatorium (Ingaóra) elküldését, már célzott erre a hipotézisre.
„S remélem, nem fognak arra kényszeríteni, hogy nyomtatásban jelentsem ki: nem értem saját hipotézisem nyilvánvaló matematikai alapjait. De tegyük fel, hogy később értesültem róla Hooke-tól, akkor is épp olyan jogom van hozzá, mint az ellipszishez.”
Kepler is, Hooke is csak sejtették, amit ő bizonyít. A Principiát három könyvre tervezte, a másodikat a múlt nyáron fejezte be,
„a harmadikból még hiányzik az üstökösök elmélete. A múlt őszön két hónapot töltöttem eredménytelen számításokban jó módszer híján, ami később visszatérített az első könyvhöz és kibővítettem azt különféle propozíciókkal, amik részben az üstökösökre, részben más, a múlt télen talált dolgokra vonatkoznak. A harmadikat (ti. könyvet) mostmár vissza fogom tartani. A filozófia olyan szemtelenül veszekedő Hölgy, hogy az ember akár törvényszéki ügyekbe keveredjen, ha vele kezd. (The third I now designe to suppress. Philosophy is such an impertinently litigious Lady that a man had as good be engaged in Law suits as have to do with her.) Ezelőtt is annak találtam, s mostmár nem közeledek felé többé, amég nem hív. Az első két könyvet a harmadik nélkül nem nagyon illeti meg a Philosophiae naturalis Principia Mathematica cím, és azért megváltoztattam így: De motu corporum libri duo (Két könyv a mozgásról. – A szerk.): de ismét megfontolva megtartottam az eredeti címet. Segíteni fog a könyv eladásában, amit most már, hogy az Önöké, nem akarok csökkenteni.”17
S még el se küldi a levelet, már június 20-án folytatja:
„Mióta ezt a levelet írtam, hallottam valakitől, aki olyasvalakitől hallotta, aki ott volt az Önök ülésén…”
Eddig nem akarta kiteregetni, hogy ki is ez a Hooke, de most már megmondja, az igazság kedvéért,
„hogy Borelli hipotézisét közölte saját neve alatt, és hogy ezt magának tulajdonítsa, és hogy sajátjaként egészítse ki, ez az alapja, úgy hiszem, az egész nagy hűhónak, amit csap”. (That he has published Borell’s Hypothesis in his own name & the asserting of this to himself & completing it as his own, seems to me the ground of all ye stir he makes.)18
Egyébként is, Hooke hozzájuthatott az ő, Newton, 1673-ban Huygens-hez írt leveléhez, s onnan szedhette a két erő hatására történő bolygómozgás gondolatát,
„és így mindaz, amit később nekem a nehézségről írt, lehet, hogy semmi más mint saját kertem gyümölcse. Akárhogyan is áll, nem tudta (amint könyveiből kiveszem) csak öt évvel azután, hogy bármelyik matematikus megmondhatta neki. Ugyanis mikor Huygens megmutatta, hogyan kell megtalálni az erőt a körmozgás minden esetében, megmondta nekik, hogyan kell eljárniuk ebben éppen úgy, mint bármely más esetben.”19
Különben is ő már az 1675-ben beküldött, fény természetéről írott dolgozatában kimondta volt az általános gravitáció gondolatát. És hosszan idéz az 1675-ös dolgozatából:
„»És amint a Föld, úgy talán a Nap is bőven beszívja ezt a spiritust (Spirit), hogy megőrizze a ragyogását és hogy visszatartsa a bolygókat a tőle való eltávolodástól, és akik akarják, azt is feltehetik, hogy ez a spiritus szolgáltatja vagy hordozza a Nap hevét és a fény anyagi princípiumát: és hogy a hatalmas aether-terek közöttünk és a csillagok között elegendő raktárai a Nap és bolygók eme eleségének.« Ezekben és az ezt megelőző szavakban le van írva a Föld, Nap és minden bolygók felé irányuló gravitás közös oka (common cause of gravity) és hogy ez az ok tartja a bolygókat Nap körüli pályájukon. És ez az egész filozófia, amiről Mr. Hooke azt állítja, hogy az ő pár évvel későbbi leveleiből vettem, kivéve a négyzetes arányt.”20
A kiadók megjegyzik, hogy természetesen mindebben nincs semmi precise formulation of the law of the inverse square.21
Newtonnak azonban más volt a véleménye. Szerinte, aki elgondolkozik a fenti hipotézisen, láthatja,
„hogy a gravitás felfelé csökken és a bolygó felületétől felfelé számítva nem is lehet más, mint a centrumától vett távolság négyzetével fordítottan arányos, de lefelé ez az arány nem áll. Ez akkor csak hipotézis volt, és csak mint sejtéseim egyikét tekintettem, amiben nem nagyon bíztam: de elegendően megmagyarázza Önnek, miért nem használtam a centrumba eső test tárgyalásában a négyzetes arányt. A földön hajított testek kis fel- és leszállásaiban a gravitáció változása annyira jelentéktelen, hogy a matematikusok elhanyagolják. Ezért szerepel náluk az uniformis gravitás egyszerű hipotézise. És mint matematikus, mért ne használhatnám én is gyakran, anélkül, hogy az egek filozófiájára gondolnék vagy filozófiailag igaznak tekinteném?”22
A kiadók a levéllel kapcsolatban idézik Hooke naplójának 1688/9. február 15-i bejegyzését:
„Halley-nál találkoztam Newtonnal – hiába követeltem jogaimat, mégis információmat elismerte. Érdek nem ismer lelkiismeretet: a posse ad esse non valet consequentia.”23
Halley válaszában24 biztosítja Newtont, hogy Hooke viselkedését eltúlozva adták át neki, részletezi 1684-es, Wrennel és Hooke-al való beszélgetésüket, s kéri Newtont, nehogy visszatartsa a harmadik könyvet,
„amelyben az Ön matematikai tanának az üstökösök elméletére és számos érdekes kísérletre való alkalmazása, amik, ha abból amit írt, jól sejtem, tárgyát teszik, kétségkívül befogadhatóbbá fogja tenni azt azok számára, akik matematika-mentes filozófusoknak hívják magukat, és akik sokkal többen vannak.”25
Newton engedékenyebb hangon válaszol.26 Ezeket tudva, elengedte volna az utóiratot múltkori leveléből. De a felfedezést még előbbre teszi. Azokat a propozíciókat – írja –, amiket 1684 végén Pagettel Halleynek küldött volt, még 20 évvel ezelőtt nyerte a Kepler-törvények alkalmazásával.
A Paget-levél ugyan nincsen meg, vagy legalábbis a legutóbbi időkig nem volt meg, de már a XIX. század közepe óta általában feltételezik, hogy azonos Newton De motu [A mozgásról. – A szerk.] című értekezésével, ami a Principia első két könyve magjának tekinthető.27
S most Newton újra támad. Felhívja Halley figyelmét, hogy Hooke egyik levelében célzott Halley Szent Heléna szigetén tett megfigyelésére: az inga a hegy csúcsán lassabban járt, mint a tövében, s ezt Hooke a távolsággal való csökkenés igazolására alkalmas kísérletnek vélte. S figyelmeztet rá, hogy ő, Newton, már 14–15, vagy talán 18–19 évvel ezelőtt kiszámította
„a Föld napi mozgásából az egyenlítőn keletkező felemelő erőt (force of ascent), hogy megtudja, mennyivel fog ott csökkenni a gravitás.”28
Ez a levél nagy gondot okozott a történészeknek. Egyrészt az 1666-os legenda, most pedig 14–15 év. – Nem hazudott talán csak? Egy Newton! – Nincs más mit tenni, mint feltételezni, hogy a Principia írása előtt már két ízben foglalkozott intenzíven az általános tömegvonzás és a reciprok négyzetes törvény problémájával. De miért? – A választ Florian Cajori adta meg egy hosszú fejtegetésében:29 Az első alkalommal még nem ismerte a földsugár pontos értékét, másodszor már tudta, s helyes eredményhez jutott. Eszerint legkésőbb 1672–73-ban az általános gravitáció elméletének birtokában volt. Erre utal a Huygens-hez 1673-ban írt levél is. Valóban, annak Newton is nagy fontosságot tulajdonított. Már július 27-én újra ír:30 megtalálta a Huygensnek 1673-ban küldött levél hiteles másolatát, amire hivatkozott volt és idézi.
Ezt az idézetet, amely a Huygens értelmében vett conatus alkalmazása a Hold Föld körüli, és a Föld Nap körüli mozgására, részletesen analizálta Dugas,31 s arra a következtetésre jutott, hogy a levél éppen azt bizonyítja, hogy az 1670-es évek elején Newton még nincs mechanikája teljes birtokában.
« …Il semble – írja Dugas – qu’en
la circonstance la mémoire de Newton soit quelque peu
complaissante… »32
(„Úgy tűnik – írja Dugas –, hogy a körülmények között Newton memóriája kissé önelégült.”)
Sőt, ez a Huygens levél azt a gyanút kelti, mintha a centrifugális erőt – Huygens-től vette volna. S érdekes módon erre fent idézett leveleiben mintha maga Newton is célozna.
Dugas történész-intuíciójának egyik legszebb tette, hogy itt, a látszat és a tudománytörténészek általános véleménye ellenére Newton mellé áll. Szerinte Newton indivisibilia-geometriai módszerekkel, már Huygens Horologium Oscillatoriumának az olvasása előtt, önállóan is számítani tudta a körmozgásban fellépő, befelé húzó, centrifugális erőt, lehet, hogy már 1666-ban. Lehet, hogy éppen ez volt az 1666-os nagy felfedezése? Annyi kétségtelen Dugas szerint, hogy Newtonnak a centrum körüli pályán történő mozgás befelé húzó erejének a számítására nem volt szüksége a centripetális erő fogalmára, ami Huygens találmánya, s így a Hold Föld-körüli mozgásából eredő befelé húzó erőt számíthatta a centrifugális erő nélkül is.
Newton ugyanis úgy járt el, hogy a görbevonalú pályát sokszögekből állónak tekintette, ahol a mozgó test minden sarokban egy-egy „lökést” kap, ami kiszámítható. A sokszög oldalszámát minden határon túl növelve, a pálya görbe vonalba, a végtelen sok kis lökés összege a centripetális erőbe megy át.33
S bár ez nyilvánvalóan egészen más valami, mint a tömegvonzás 1/r2 törvénye, Dugas a Hooke–Newton-levelezés részletes (de nem teljesen megbízható) ismertetése után arra a végkövetkeztetésre jut, hogy Hooke zavaros gondolkozású, kapkodó ember, akinek nincsenek a Huygens-éihez és Newtonéihoz fogható tiszta mechanikai fogalmai.34 Hooke legfeljebb ha megsejtett valamit, de a vita hevében Newton is olyasmikre hivatkozik, amik nagyon messze esnek a Principia nívójától, pl. az 1673-as Huygens-hez írt levélre, és az 1675-ös fény természetéről írt dolgozatára – vonja le analízise végkövetkeztetését Dugas.35
Nos, Dugas sejtése, hogy Newton valóban Huygens-től függetlenül jött rá a centrális erő számítására, fényesen igazolódott. A. R. Hall közölt egy „Portsmouth Collection”-ban talált Newton-kéziratból kivonatokat,36 amelyekről kétségtelennek tartja, hogy azonosak azzal a számítással, amire Newton a Halley-nek írt 1686. jún. 20. és júl 14. levelében célzott; aminek a létezését Dugas sejtette.
A kéziratban azonban sehol sincs szó centrális erőről, csak conatusról, vagyis egy mozgási centrum felé- vagy attól elirányuló tendenciáról, az erő szót csak a gravitással kapcsolatban használja. Számításai gyorsulásokra korlátozódnak, nem a létrehozott erőkre. És a földsugár itt használt értékével sem kap a Hold conatusából számított földi gyorsulásra semmivel se jobb értéket, a „legendás” 1666-os.
Cajori hosszú spekulációi a probléma kétszeri megközelítéséről összeomlanak – írja Hall. Newton az 1670-es évek elején sem ismerte jobban a földsugár helyes értékét, mint 1666-ban. A dokumentum semmi bizonyítékot se hoz arra, hogy írása idejében birtokában lett volna az 1/r2 törvénynek vagy az általános gravitációnak bár olyasmi sincs benne, ami inkompatibilis lenne ezzel a feltevéssel, és Newton esetében the argument from silence is never strong.37
Sajnos, a kéziratot nem lehet pontosan időzíteni – fejezi be közleményét Hall – de feltehetően a 70-es évek elejéről származik, s épp ezért rombolja le a Cajori-hipotézist.
A Newton-levelezés tudós kiadója, Turnbull professzor, már időzíthetőnek ítéli a kéziratot: 1665 vagy 1666-ra.38 Azért tartja különösen fontosnak a kéziratot, mert
„egy idáig nem is sejtett láncszemet jelent Newton és Galilei munkája között.”39
Ezek a feljegyzések egyenesen Galilei első olvasásának a hatására keletkezhettek. Talán Thomas Salusbury Dialogo-fordítását40 olvashatta Newton, a számításokat mindenesetre az ott talált numerikus példákra alapozza, s a nehézségi gyorsulás ingalengésből való meghatározását is onnan veszi.41 J. W. Herivel pontosan meg is mondja: a számpéldákat Salusbury Dialogo-fordításának a 200. oldaláról vette.42 A kézirat Herivel és a levelezés kiadói szerint három mozgásféleség gyorsulásának a számítását tartalmazza: 1.) a köringáét, 2.) a köralakú pályán Nap körül mozgó Földét, és 3.) az egyenlítő egy pontjáét.
Az utóbbi különösen érdekes. Newton erre vonatkozó számításait összefoglalva leszögezi, hogy
„a gravitációs erő 159,5-ször nagyobb, mint a Föld forgásából az egyenlítőn keletkező erő.”
(“Ye force from gravity is 159.5 times greater
yn ye force from ye Earth’s motion at ye Equator.”)43
Jogosan háborodott fel Newton: ő ne ismerte volna, hogy az egyenlítőn – a Szent Ilona szigetén – csökken a gravitáció? Jogosan? Hooke ugyanis nem ezt állította rekriminált levelében. Hooke nem azt emelte ki, hogy Szent Ilona szigete az egyenlítőn van, hanem azt, hogy történetesen Szent Ilona-sziget egy magas hegycsúcsán Halley lassabbnak találta az inga mozgását, mint a hegy lábában. S felveti, nem lehetne-e ezt a tényt felhasználni annak a kísérleti eldöntésére,
„vajon a gravitás tényleg csökken-e a centrumtól nagyobb távolságra. Ennek a vizsgálatára régebben számos kísérletet végeztem a Szt. Pál tetejéről és a Westminster Apátságéról, de egy se volt meggyőző.”44
A Hooke–Newton-levelezést és a vitát követve, ugyanez a tendencia ötlik mindenütt szembe: Hooke mindig a centrális vonzáshoz ragaszkodik makacsul, Newton mindig ügyesen kitér a centrális mozgás felé. A kitérés egyik oka most már nyilvánvaló: a centrális mozgás törvényeit valóban sokkal előbb ismerte, mint Hooke, már 1666-ban, közvetlenül Galileihez csatlakozva. Amikor tehát 19–20 évvel azelőtti felfedezéséről beszél, nem hazudik, formálisan legalábbis nem hazudik: amit állít, a centrális mozgás gyorsulását valóban kiszámította.
Ez természetesen semmit sem mond arra a kérdésre vonatkozóan, ismerte-e a tömegvonzás 1/r2 törvényét is. Számunkra a dolog olyan egyszerűnek látszik. De Huygens is nagyon jól ismerte – sokkal jobban, mint az 1666-os Newton – a körmozgás törvényeit, mégsem jut el soha belőlük az általános tömegvonzás gondolatáig. Herivelnek az interpretációja szerint a fenti Newton-kézirat
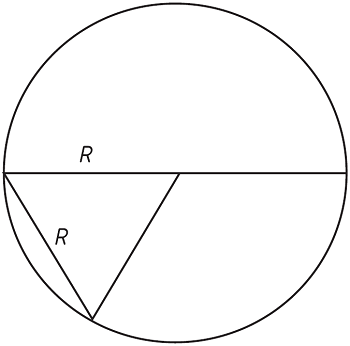
„A centrifugális erő valamilyen világosabb megértését megelőző két primitív számítással kezdődik, s azután kiszámítja a két arányt (ti. a gravitációs erőnek a Föld napi és évi mozgásából eredő centrifugális erőkhöz való arányát) az alábbi eredmény implicit felhasználásával: Ha egy test egy R sugarú körön történő mozgás centrifugális erejével egyenlő erő hatása alatt mozog egyenes vonalon a középpont felé, akkor ugyanannyi idő alatt, ami alatt a körön mozogva R távolságot tett meg, az egyenes vonalban R/2-t.”45
Ezt az implicit eredményt egy 1666. május 16-os keltezésű kézirata – amit szintén a Correspondence ad ki először – explicite is kimondja.46 A kézirat jelentősége óriási: a körmozgás egyszerű analízisén túl tartalmazza Newton infinitezimális elképzeléseinek a csíráit. Szinte kézzelfoghatóvá teszi a newtoni mozgásgeometria genezisét.
A kézirat egy 1670-es évek elejéről, valószínűleg 1672-ből származó bővítése és javítása: The lawes of Motion. How solitary bodyes are moded47 pedig már valóságos „ős-principia”, legalábbis az első két könyv bizonyos propozícióit illetőleg. Nagyon figyelemreméltó, hogy már itt megvan az abszolút tér gondolatának a csírája, de még nem mint absztrakt, matematikai entitás, még kevésbé, mint „isten sensoriuma”, hanem egyszerűen mint „uniform extension”. De már benne vannak a testek, már nem az extensio jelenti a testek substantiáját, mint Descartes-nál.
A tér még csak a testek és a mozgás – elsősorban a körmozgás – színpada, nyoma sincs még benne annak a fenséges, abszolút jellegnek, amit a Principia második kiadásának Scholium Generale-jában kap meg.
Hiányzik ehhez egy óriási, központi jelentőségű, mindent elrendező törvény: az általános tömegvonzás törvénye.
Hiányzik még csírájában is a Principia harmadik könyve. Az a harmadik könyv, amely ennek a törvénynek a diadalútja, az új világmindenség kodifikációja és bibliája. A Harmadik könyv, amit Newton legkésőbb írt meg saját levelei szerint is, aminek a tükrében az első könyvön is változtat, amelyiket inkább visszatart, de amelyikben nem enged egy talpalatnyi-jogot se senkinek. Amelyiknek a keletkezését egyre előrébb teszi: 8–9 év, 14–15 év, 18–19 év, – végül öregkorában visszaemlékezve: 1665–66. A Harmadik könyv, amelyik az alma-mese vulgárisabb vagy tudományosabb megfogalmazásával Newtont az Új Világ Prófétájává avatta.
Newton nem tévedett. Nagyon jól tudta, mihez kell körömszakadtáig ragaszkodnia.
Akkor is, ha nem az ő szellemi tulajdona? Vagy nem csak az övé? Pontosabban: nem teljesen magától jött rá?
Mert hogy Hooke az alaptörvényre – nem többre, de nem is kevesebbre – magától jött rá, az biztosnak látszik. – Miért nem Robert Hooke lett a „Próféta”?
Ezt kérdezte Louise D. Patterson, Hooke egyik késői védelmezője. Két nagy feltűnést keltő cikkben analizálta Hooke gravitációs törvényét és Newtonra való hatását.48 Kimutatja Hooke levelei és munkái alapján, mennyire tisztában van már az 1670-es évek végén Hooke az általános gravitáció lényegével és jelentőségével, milyen nyíltan közli felfedezését Newtonnal, aki egyszerűen felhasználja a tálcán nyújtott 1/r2 törvényt; éppen ez hiányzott a rendszeréből. Azért igyekezik később befeketíteni Hooke-ot, hogy ezzel elfedje, hogy tőle vette az általános gravitáció eszméjét és az 1/r2 törvényt. Ezért datálja egyre előrébb a törvény „felfedezését”, míg 1665–66-nál áll meg: a bölcsőig mégsem mehet vissza.
Newton nyomán feketíti máig Hooke-ot az utókor. Mint intuitív experimentátort szokás beállítani, – Newton nyomán – aki matematikához semmit se értett. Pedig inga és rugó vizsgálatai is arra utalnak, hogy kellett matematikai ismereteinek lennie. Csak hallatlan ötletgazdagsága miatt egyik ötletét se tudta kidolgozni, s nagyrészt felkapkodták a többiek, – Newton is. A Royal Society valósággal az ő ötleteiből élt.
Hooke ne értett volna a matematikához? S itt – a hagiográfusok szokása szerint – L. D. Patterson is túllő a célon: Szerinte meg lehet találni Hooke-nak az ingamozgásról szóló írásában a
„mozgás második törvényét az alábbi formában: »a vibratio sebességének a meghatározása a strength mennyisége és a mozgatandó test nagysága (bulk) közötti aránytól függ« vagy modern nyelven, »a sebesség meghatározása az erőnek (force) a tömeghez (mass) való arányától függ«. Kétségkívül ez volt a későbbi mozgás-differenciálegyenletek őseinek az egyike.”49
És még T. L. More – a világhírű Newton biográfus – azt meri állítani, hogy a Newton ellen felhozott plagizálási vádak hamisak! –
„Newtonnak az volt a szerencséje, hogy túlélte riválisait, és hosszú ideig uralkodó befolyása volt azokat követő, náluk kisebb tudósok társaságában.”50
Nos, kétségtelen, hogy volt egyéb „szerencséje” is, többek között az, hogy az erő és a tömeg fogalmát csak ő fogalmazza meg olyan tisztán, hogy Patterson kisasszony Hooke bizonytalan megsejtését játszi könnyedséggel fogalmazhassa át velük – differenciálegyenletté. Hooke kétségkívül rendelkezett bizonyos matematikai érzékkel, de matematikus, s éppen olyan, aki a differenciálegyenleteket megsejtse, amiktől felfedezőjük, Newton is úgy megijedt, hogy egy életen át elrejtette őket, nos, ilyen matematikus kétségkívül nem volt.
Koyré professzornak nem volt nehéz kimutatni, mennyire nem reális túlzásba csapott Hooke védelmében Patterson.
Hooke – Koyré szerint – először is téved az ingamozgás kiszámításában, amit L. D. Patterson olyan dicsőséggel idéz. S ha rá is jön – Huygens nyomán! – 1679 körül a fordított négyzetes törvényre, nem tud vele mit kezdeni: nem tudja levezetni segítségével a bolygók ellipszis-pályáját. A gravitáció Holdra való kiterjesztésével pedig Kepler Astronomia Novajában (Új asztronómia. – A szerk.; 1609) és W. Gilbert De Magnete-jában (1600; A mágnesséről. – A szerk.) találkozunk. Hooke ebben nem anticipálta Newtont. S nem anticipálta főleg abban, ami nem volt neki: matematikai gondolatokban. Hooke-nak nem volt meg a szükséges matematikai ismerete,
„ami csak azzal magyarázható, hogy hiányzott belőle a kísérlethez való matematikai közeledés alapvető értékének a megértése. Optikában éppúgy mint fizikában, Hooke mindig csak egy baconiánus volt és maradt.”51
Láttuk, hogy lényegében Koyré véleményét vette át ebben a kérdésben René Dugas is.
Hooke ügyét ismét egy nő – Margaret Espinasse – karolta fel. Robert Hooke-ja (London, 1956) valóságos „Hookeiada”.
Gerd Buchdall szerint azért mégse volt Hooke mártír, mint ahogy Espinasse rajzolja. Inkább egyfajta „mindent kipróbálni” optimizmus volt benne, ami egybevágott a Royal Society kezdő éveinek progresszív, felfelé ívelő, „protestáns” prakticista tendenciáival.52
Valójában Hooke se szent nem volt, se mártír, se optimista, se „protestáns”. Milyen volt Robert Hooke? A világirodalom egyik legérdekesebb könyve, a híres Diary53-ja (Napló. – A szerk.), amit 1935-ben adtak ki először, felel a kérdésre.
Hooke apja szegény curator volt a Wight-szigeti Freshwaterban, s 13 éves volt Hooke, mikor apja meghalt. Örökségét arra fordítja, hogy a londoni Westminster School-ba iratkozzék be, ahol Euklidész első 6 könyvének egy hét alatt való megtanulásával tűnik ki. 1653-ban kerül kóristaként – kisebb fajta ösztöndíj – az oxfordi Christ Church-be: Wilkins tiszteletes úr felismeri a tehetségét, s ad egy példányt páratlan Mathematicall Magick-jából a fiúnak. Szerencsére hathatósabb segítségben is részesíti: bejuttatja Dr. Thomas Willis mellé kémiai kísérleteket Seth Ward mellé asztronómiát tanulni. Willis ajánlja Boyle-nak, aki asszisztensekkel dolgoztat. De Hooke nemcsak egyszerű asszisztens: Euklidészt és Descartes-ot is magyarázza főnökének. Boyle-al végig jó barátságban marad: Boyle ráhagyja mikroszkópját, mágnesét és egyéb „experimentális” apróságait.
1662-ben „Curator of experiments” a Royal Society-ban. Hetenként két új kísérletet kell kigondolnia és bemutatnia az „experimental philosophers” kísérlet-éhségének a kielégítésére. Szerencsére az akkori kísérleteket kigondolni és elvégezni egyaránt könnyebb volt, mint a maiakat, de még így is pokoli elfoglaltság. – Biográfusa és kiadója, H. W. Robinson szerint
„Alig túlzás azt állítani, hogy ő volt a Royal Society történelmi megteremtője.”54
1664/5 márciusában geometria professzornak választják a Gresham College-ba. Egyike azon kevés korabeli professzoroknak, akik pontosan ellátták előadásaikat.
1665-ben jelenik meg Micrographiá-ja. Akiknek módjukban volt látni ezt a könyvet, s nem elfogultak Hooke-al szemben, egyöntetűen azt állítják, hogy a kor egyik legjelentősebb műve, talán még a Principiával is vetekszik.
„…Hooke csaknem a legtermékenyebb feltaláló géniusz volt, ha ugyan nem a legtermékenyebb, aki valaha élt, és legalább egy könyvei közül, a Micrographia, a tudományok történetében a legfontosabb valaha is publikált könyvek között van.”
– írja bibliográfusa, G. Keynes.55
Az a rövid ismertetés és a pár gyönyörű ábra is, amit Keynes közöl, meggyőzhet bárkit arról, hogy nem túloz. A mikroszkópot éppúgy Hooke fedezte fel a tudomány számára, mint ahogy a távcsövet Galilei.
De a Micrographia sokkal több mikroszkopikus ismeretek leírásánál és rendszerezésénél. Számos kémiai kísérlet leírását is tartalmazza és többek között korának legjobb égéselméletét adja, ami sokak szerint közel jár az Oxygén felfedezéséhez,56 először ajánlja a fagyáspontot hőmérők standardizálására, modern módon tárgyalja a kristálystruktúrákat, gömbökből készült modellek segítségével; a thermikus expansiót az anyag általános tulajdonságaként ismeri fel, s a hőt a corpusculák mozgására vezeti vissza. Leírja a vékony lemezek színeit és felismeri, hogy azok a két felületről visszavert fény keveredésére vezethetők vissza.
Foglalkozik a könyv számos, Hooke által feltalált meteorológiai műszer leírásával is, s a kísérleti meteorológia megalapításának tekinthető.
S ha mindehhez hozzávesszük, hogy a légszivattyút is Hooke tette tudományos kísérletekre alkalmas műszerré, s hogy állítólag a Boyle-féle gáztörvényt is ő fedezte fel,57 valóban nem túlzás azt állítani, hogy az „Experimental Philosophy” igazi megalapozója Hooke.
S ezen túl egy egészen újfajta tudós-típus megszemélyesítője.
Az 1666-os londoni nagy tűzvész után a három City Surveyor egyike, működése messze a felmérésen túl a város rendezésére, köz- és magánépületek építésére is, kiterjed. Ő és Wren adták meg a mai London városképének az alapját. Hooke építette a Bedlam Hospital-t, a Montague House-t, a Merchant Taylors Hall-t, a College of Physicians-t, Lady Ranalagh (Boyle nénje) és sok városi tanácsos házát.
Van az épületeiben minden racionalitásuk mellett valami kiszámíthatatlan, szinte azt mondhatnánk, „kamaszos” báj. Nem „szépek” – abban az értelemben, ahogy a kontinens korabeli épületei, a nagy francia Louis XIV vagy az itáliai barokk szép. A Wrennel kapcsolatban hangoztatni szokott „Latinity” Hooke-nál még inkább angol – nem, londoni – jelleget ölt, mint Wrennél. A Principatus Rómája – mint egykor Firenzében a Leonardo Bruni nemzedékének a Köztársaságé – politikai, gazdasági, művészeti és „életstílus” eszmény lesz. A XVII. század második felének a Londonja közelebb van az antik Rómához, mint bármely más európai város. Egy nagy birodalom szíve kezd itt is egyre erősebben verni, de ezt a szívet a nagy szárazföldi utak helyett a végtelen tengerek sós lehelete táplálja.
Fantasztikus karrierek: London egyik legjelentősebb polgára, John Collins (1624/5–83), Newton, J. Gregory, Wallis barátja, F. R. S., a Royal Society annyi értékes tudományos levelezésének a lebonyolítója, könyvkereskedő-tanoncként kezdi, aztán évekig harcol velencei hajókon a törökök ellen, visszatérve matematika tanár lesz, majd állami hivatalnok, a Council of Plantations (Gyarmatügyi Tanács) titkára – s emellett állandóan talál időt nemcsak arra, hogy ő maga komolyan, alkotó módon foglalkozzon matematikával, hanem arra is, hogy szünet nélkül, bátorítsa és segítse kevesebb életenergiával megáldott tudóstársait.
A Restauráció Londonja számára életszükséglet volt a természettudomány. Száznál több kávéházának mindegyikében állandó téma az új „Experimental Philosophy”, s mindegyikében megfordul, néha egy nap többen is, a fáradhatatlan Dr. Hooke, hogy megigya a maga csokoládéját vagy „rövidebb” italait, s pontosan bejegyezze naplójába:
„1675. november 4. Felolvasás a gyertyáról és a súllyal állandósított lámpáról, és bemutattam a kísérletet a csillámüveggel és a lánggal. A Garavay-kávéházban, Hoskins, a fiatal Cambridge-i tudós, Tompion, Adamson. Csokoládét ittam. Jalápgyantát tettem borszeszbe, hogy reggel bevegyem, de nem vettem be, mert egész éjszaka nagyon rosszul voltam, de sok sört ittam és a műhelyben dolgoztam, ami szörnyen jót tett.”58
Rengeteg könyvet vesz magának is, a Royal Society-nek is. Érdeklődése igen széleskörű. Matematikától és mechanikától alkímiáig és művészettörténeti könyvekig mindent vesz. Sokszor fordul elő a naplóban Vitruvius, Heron, Galilei, Schooten, Harriot. De megveszi Paracelsus Philosophiá-ját és Glauber De mercurio philosophorum-át (A filozófusok higanyáról. – A szerk.) is. Feltűnő, milyen sok francia könyvet olvas, s főleg milyen nagy gondja van a Journall de Scavans, a rivális lap rendszeres beszerzésére, olvasására és kölcsönzésére.
Sok – különösen télen – az időjárásra vonatkozó bejegyzés. Tulajdonképpen az egész Napló rendszeres időjárás-feljegyzésként indul. Később már az ebédeit és szeretkezéseit is beírja. Nell, Dol, Mary – szolgálói – és a 70-es évek közepétől unokahúga, Grace Hooke (1659?–87) … Gracenak könyvre £ 6 2 1/2 sh.59 … Grace-t Nell látta valakivel. Grace tagad. …
Things not right.60 – De aztán rendbe jön minden és Grace – úgy látszik – haláláig hűségesen szereti.
Rugók, órák, távcsövek, legkülönfélébb műszerek, gyűlések, kávéház, akadémiai tisztségek és elismerés után való törtetés, egyetemi előadások, hajsza a Pénz után, könyvek, építés, nők: a nagyváros életének lármája, izgalma, boldogsága és gyötrődése kerül Hooke naplójában kézzelfogható közelségbe. Egy új életforma: az újkori nagyváros természettudósának az életformája tükröződik Hooke naplójából.
Ebben a forgatagban születik meg az általános tömegvonzás gondolata Hooke fejében, erről beszél már 1674-ben egyetemi előadásain, erről beszélget Wrennel a Szent Pál székesegyház építése közben, a kávéházakban.
„…1677. szeptember 20. Sir Chr. Wrenhez, a Szt. Pálba, találkoztam vele a Greshamben, Jonathans-hez (híres kávéház). Beszélgettem vele a Hold-elméletről. Azt állította, hogy, ha a mozgás fordított arányban állana a távolsággal, a sebesség mindig úgy aránylana, mint a területek, bármi legyen is a görbe…”61
Hooke ekkor ennél már sokkal többet tudott. De azt nem Sir Christophernek mondotta el, hanem – Isaac Newtonnak.
Isaac Newtont nem lehetett nagyon elfoglalt embernek nevezni. Csak az év végi trimeszterben kellett előadnia, heti egy órában. Mindig saját vizsgálatairól beszélt, és előadásai a 80-as évek elején, 70-es évek végén optikáról szóltak.
Már negyven felé járó, nagy-nagy köztiszteletben álló, a matematikában világhírre szert tett tudós volt. Mögötte van a színekről folytatott nagy vitája és híres levélváltása Leibniz-cal, a tudományos diplomáciának ez az iskolapéldája, ahol mindketten úgy akarták kicsalni a másikból a sejtett tudását, hogy a magukéból semmit ne áruljanak el. … Matematikusok és matematikatörténészek generációit vezették félre ezek a levelek. De Leibniz – legalábbis Newton attól félt – többet értett meg belőle a kelleténél. Ez a félelme talán nem is volt olyan alaptalan.
S akkor ez a folyton nyüzsgő Hooke, gyanúsan őszinte leveleivel…
A Royal Society új titkára. A „Nagy Experimentátor”. A Newton által is nagyon tisztelt Boyle barátja. A király is többször, személyesen megdicsérte óráját. De a matematikához, az igazi „Experimental Phylosophy” kulcsához nem ért. Legokosabb az ilyet udvarias formasággal lerázni. Bolygók mozgása egy központ felé mutató vonzóerő és egy tangentiális erő együttes hatása esetén … Hányan próbálkoztak már ezzel a „Philosophical World”-ben, még ő is, réges-régen. amikor a körmozgás kérdése izgatta…
De felad egy kis matematikai példát a londoniaknak. – Mennyit dobálták a század közepén tornyok tetejéből a köveket annak az eldöntésére, forog-e a Föld. Az artistoteliánusok ugyanis azt állították, hogyha forogna, akkor, amíg a kő esik, a Föld nyugat–kelet irányban mozogva „kifarolna” alóla, s a kő nem a torony aljába, hanem attól nyugatra esne le. A galileisták viszont állították, hogy a mozgó Földön is a torony tövébe kell esnie, mert átveszi a Föld mozgását. Mint ahogy a sebesen száguldó hajó árbocáról leejtett kő is az árboc tövébe esik.
De Newton már régen tudta, hogy a körmozgást nem lehet az egyenes vonalú, egyenletes mozgással azonos módon tárgyalni. A körmozgás másféle mozgás.
„Igazibb” mint az egyenes vonalú egyenletes mozgás. Abszolút. A torony tetejéről leejtett kő nem eshet a torony tövébe, mert a nyugat–kelet irányba forgó Föld „meglökte” érintője irányában kelet felé. A kő kelet felé fog eltérni, s ha a pályája a föld alatt is folytatódna, csigavonalon a Föld centrumába esne.
Hooke lelkesedik, de korrigál. Nem keletre, hanem délkeletre tér el, és a Föld belsejében sem olyan a pálya, mint Newton írta. Egy centrum felé vonzódó érintőleges mozgással is bíró testnek nem kell a centrumba esni: ha nincs közegellenállás, ellipszisen fog mozogni a centrum körül.
Newton most számol: valóban van ilyen lehetőség. De nem ellipszis, hanem egy bonyolultabb vonal. De Hooke más feltevésből indul ki, abból, hogy a centrális vonzás a távolság négyzetével fordított arányban csökken, s szerinte ez az egyszerű feltevés magyarázza meg valahogy az egész bolygórendszer mozgását, csak éppen azt nem tudja, hogy hogyan.
Jellemző ez a londoni „philosophusokra”. Hipotéziseket állítanak fel „a jelenségek megmentésére”, s nem tudják igazolni azokat. Legjobb ezektől elszakadni, Newton tudta előre. …
Flamsteed, a greenwichi csillagász egészen más jellegű tudós, mint a „zavaros”, kapkodó Hooke. Pontos, türelmes, lelkiismeretes, megbízható megfigyelő és amellett milyen tiszteletteljes…
A megilletődés, a tisztelet és a nagy felfedezés feletti öröm keveredik a levelében, amit 1680. dec. 15-én ír Newtonnak.62 A november elején itt járt nagy üstökös újra-megjelenéséről számol be. A novemberi üstökös szokatlanul nagy sebességgel haladt a Nap felé. Flamsteed a novemberit nem látta, de azonnal gondolta, hogy miután elhaladt a Nap közelében, újra meg fog jelenni.
„…eszerint várva rá – írja –, múlt pénteken az Aquila alatt megpillantottam egy igen kis farkat.”63
A kis farok azonban szokatlanul gyorsan kezdett növekedni, dec. 29-én az üstökös már újra a Föld közelébe ért, 1681 januárjában már távolodni kezdett. Az üstökös szokatlanul nagy sebességgel mozgott a Naptól a Föld felé.
Senki nem kételkedett benne, hogy két üstökösről van szó. Az akkor uralkodó Kepleri felfogás szerint az üstökösök ugyanis egyenes vagy alig hajlott pályákon haladtak el a Nap mellett, s elképzelhetetlen volt, hogy az 1680 novemberében oly nagy sebességgel a Nap felé száguldó üstökös azonos lenne a decemberben megjelent, Föld felé tartó üstökössel. Ehhez olyan mértékben hajlott pályát kellett volna feltételezni, amit elképzelhetetlennek tartottak.
Igaz ugyan, hogy a koppenhágai csillagász, Hevelius, 1668-ban megjelent Cometographia (Üstökösleírások. – A szerk.) című művében már feltette a kérdést, nem mozognak-e az üstökösök a Nap közelében hajlított, esetleg parabolikus pályán, de a tudományos közvélemény ezt nem vette komolyan: Különösen nem Angliában, ahol Heveliusról egyébként se tartottak sokat. Hevelius (1611–87) ugyanis régi vágású csillagász volt; s kardoskodott a puszta szemmel való helymegfigyelés előnyei mellett. Angliában pedig éppen Hooke, Newton, Flamsteed munkája nyomán óriási lendületet vett a műszeres csillagászat és a teleszkópos helymegfigyelés.
Senki se hitte komolyan, hogy a novemberi és a decemberi üstökös azonos lehet. Csak Flamsteed. Ő ugyanis elmulasztotta a novemberi üstökös észlelését, s most alig várta, hogy újra megjelenjen. S mikor megjelent, elsőnek értesítette róla a nagy Newtont. Tévedett volna? – De miért ne lehetne az üstökös pályája ennyire hajlott? Ha a Nap óriás-mágnes, amelyiknek az örvénye (vortex) mozgatja a bolygókat, s ha feltesszük, hogy az üstökös egy kis mágnes, s még hozzávesszük azt a régi „tapasztalatot”, hogy az ágyúgolyó röpülés közben magától sohasem fordul meg, akkor az egész dolog könnyen érthető. Az üstökös, ez a kis mágnes bekerül a Nap vortex-ébe, ami megfordítja, a másik pólusát fordítja a Nap felé, s ha az előbb a Nap vonzotta, most taszítani fogja.
Akárhogyan is van – írja Flamsteed – a Nap vonzza a bolygókat, and all like bodys that come within our Vortex.64
Az üstökös egyre jobban izgatja Newtont. Hosszú levélben válaszol Flamsteednek.65 Megköszöni és Flamsteedre hárítja vissza a kapott bókokat, dicséri pontos munkáját. Ami azonban a hipotézist illeti … az üstökös semmiképpen sem mehet el a Nap alatt, amint Flamsteed hiszi.
„Az eset ugyanaz, mintha egy ágyúgolyót lőnének ki nyugat–kelet irányba.
A Föld vonzása gravitásánál fogva (The attraction of ye earth by its gravity) az ágyúgolyót egyre inkább lefelé irányítja, de sohasem teszi egyenesen lefelé tartóvá, még kevésbé fogja megfordítani keletről nyugatra. Az örvény mozgása sem segít a nehézségen, még inkább növeli.”
Az örvény ugyanis ellenkező irányba, a Naptól elfelé terelné az üstököst.
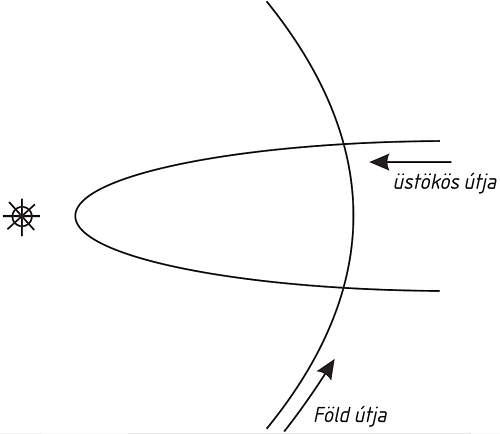
„Az egyetlen út, amely véleményem szerint segít ezen a nehézségen, az a feltevés, hogy az üstökös nem a ☉ és a Föld között ment el, hanem megkerülte a Napot (to have fetched a compass), mint ezen az ábrán.
Másodszor, bár azt könnyen feltehetőnek tartom (I can easily allow), hogy a Napban egy vonzó erősség (attractive power) van, ami által a bolygókat körülötte történő járásukban megóvja az érintő egyenesekben való elmenéstől, de azt, hogy ez a vonzás mágneses természetű lenne, kevésbé vagyok hajlandó elhinni…”66
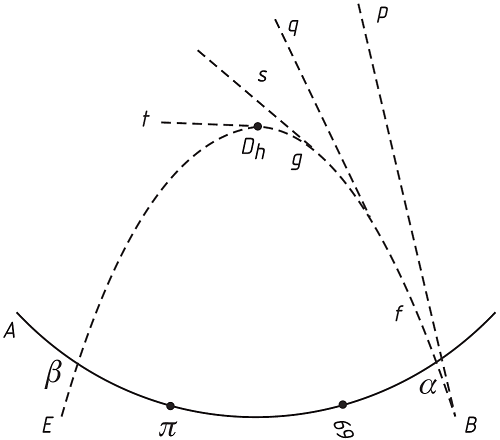
A tapasztalat ugyanis egyértelműen arra mutat, hogy a mágneses testek felhevítve elvesztik mágnesességüket, márpedig a Nap nagyon forró … S ami még sokkal lényegesebb: a mágnes előbb mindig irányít, s csak aztán vonz, s ha egyszer magához vonzotta a kisebb mágnest, azt többé nem taszítja, el se engedi. A mágnesség elsősorban irányítást jelent, hangoztatja Newton. S különben is, ha a Nap mágnességgel tartaná magához a bolygókat, azok tengelyének mind egyirányba kellene mutatni, mint a Földön a mágnestűknek.
Egyébként is Newton arra gyanakszik,
„hogy a novemberi & decemberi üstökös, amiket Mr. Flamsteed egy és ugyanazon üstökösnek tart, két különböző üstökös.”67
Ugyanis túl szabálytalan a mozgása ahhoz, hogy egy pályába lehetne összefogni. Itt vannak például Gallet atya római észlelései … Azokkal mit csinál Flamsteed?68
Végül kéri, küldjön továbbra is pontos jelentéseket az üstökös helyzetéről, s ne vegye zokon, amiket a hipotéziséről írt. – Egyébként a Flamsteed elméletében van egy csomó elfogadható tétel is, pl. hogy a farok híg gőzből áll (thin vapour), hogy a farok a fej körüli atmoszférából ered, hogy a Nap fénye okozza a felemelkedését, hogy a Nap fényét visszaverve világít, s nem saját magától.69
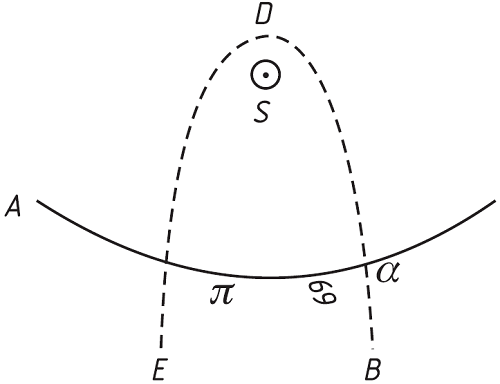
Flamsteedet azonban ez nem vigasztalja: őt az üstökös útja érdekli, nem a farok. Nagyon tiszteletteljesen, de nagyon határozottan szembeszáll Newton véleményével.70
„Mr. Newton nagyon lekötelezett geniális és világos észrevételeivel, amiket a most elvonult üstökös jelenségeinek a megmentésére felállított propozícióimra tett. Be kell vallanom neki, hogy rövidesen közölni szeretném megfigyeléseimet, de ugyanakkor, ami ezeket a fizikai dolgokat illeti, azok egyikével se tudok szembeszállani, mert szeretem a békességet, és nagyon jól tudom, milyen bajt hozhatna rám egy ilyen, saját területemen kívül eső publikáció. Csak az igazság szeretete és ezen jelenségekkel szemben általánosan elfoglalt vélemény nem tetszése késztetett arra, hogy üres óráimban gondolkozzam, mi lehet ezeknek a valódi természete. És mikor úgy véltem, hogy felfedeztem valamit, ez arra késztetett, hogy elküldjem Önnek és hogy megtudjam Mr. Newton érzéseit (sentiments), akinek az enyémtől eltérő véleménye, be kell ismernem, nem kis előnyömre szolgált, mert számos további argumentumot juttatott eszembe véleményem (opinion) védelmére, amikre egyébként aligha gondoltam volna.”71
Flamsteed 1646-ban született, ugyanabba a generációba tartozik, mint Newton. Hooke a megelőzőbe. Hooke udvarias hangján is érződik az egyenrangú. Flamsteed tudja, hogyan kell Mr. Newtonnal beszélni.
Ami az üstökös mozgásának a „szabálytalanságát” illeti – írja Flamsteed – Newton téved. Elnézte, hogy Gallet, akinek a megfigyeléseire Newton hivatkozik, a régi naptár szerint adta meg azokat, s azért látszanak a többi közül kiugrani.72
Abban viszont igaza van Newtonnak, hogy a pálya valóban a Napon túl hajlik vissza, az adatok egyértelműen erre mutatnak. És Flamsteed csatol egy merész szerkesztést – pár megfigyelése alapján!73 – az üstökös valódi, térbeli pályájáról.
Ami a nagy mágnest illeti, valóban irányít mielőtt vonzana, igaza van Newtonnak. De ez is csak akkor szólna ellene, ha Newton be tudja bizonyítani,
„hogy egy nagy álló mágnes ugyanígy hatna egy mellette vagy körülötte hevesen eldobott kis mágnesre is.”74
Newtont egyre jobban izgatja a „két” üstökös. Maga is pontosan követi a decemberit, amíg csak látni lehet, fonalkeresztes teleszkópjával, s gyűjt minden rávonatkozó megfigyelést.75
A pontos megfigyelésre helyezi a hangsúlyt. A lehető legpontosabban rekonstruálni kell a két üstökös térbeli, valódi, „abszolút” mozgását, az üstökösöknek az ekliptikához való hajlása látszólagos sebességüket nagyon megváltoztathatja. Amíg nem ismerjük a két üstökös igazi pályáját, nem lehet semmit mondani.
Az pedig, hogy a nagy mágnesnek a kis mágnesre való irányító hatása erősebb, mint a vonzó, kísérleti tény, itt nincs mit teoretizálni. Az elhajított mágnes? – a mágnestű a leggyorsabban száguldó vitorláson is ugyanarra mutat, mint az állón.
Lám, Newton, az „empirista”. Vagy mégse?
„Az, hogy az ágyúból kilőtt golyó mindig ugyanazt az oldalát fordítja előre, régi tüzér-tradíció lehet, de nem tudom belátni, hogy egyeztethető össze a mozgás törvényeivel (laws of motion) és azért merem állítani, hogy megfelelő kipróbálás esetén nem így fog történni, kivéve néha, véletlenül.”76
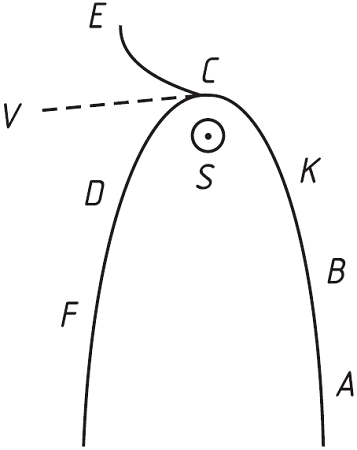
Tapasztalat ide, kísérlet oda, csak az a mozgás „valóságos”, ami összeegyeztethető a „mozgás törvényeivel”. Vajon a Flamsteed hipotézise – hogy ti. a két üstökös egy – összeegyeztethető-e a mozgás törvényeivel? És egyelőre csupa kifogásokat hoz fel. Mert ha a Nap vonzaná felé haladtában, és taszítaná távoztában az üstököst, akkor a taszítás alatt is egyre gyorsabban kellene mozognia, márpedig a megfigyelés azt mutatja, hogy a decemberi üstökös egyre lassabban jár.
Másik kifogás: Mikor az üstökös C-be ér, itt se vonzás, se taszítás nem lehet, ez a vonzás és taszítás határa. Ha bármily kicsit túlmegy D felé, ott már taszítás érvényesülne, s akkor nemhogy D felé haladna, hanem elrepülne E felé.
„De mindezek a nehézségek elkerülhetők, ha feltesszük, hogy a Nap mágnessége irányítja és vonzza az üstököst, és ezáltal épp annyira késlelteti távozásában, mint amennyire gyorsította közeledésében. És ez a folyamatos vonzás egy kerülőt tétet vele a Nap körül ABKDF vonalban, C-ben a vis centrifuga túlsúlyba jut a vonzás felett és arra kényszeríti az üstököst, hogy a vonzás ellenére is távolodni kezdjen a Naptól.
Az üstökös pályájára vonatkozólag még nem végeztem számításokat, bár azt hiszem, van erre egy közvetlen módszerem, bármi legyen is a mozgás pályája.”77
1681. ápr. ? – Az új világrendszer „qualitativ” születésnapja? A „mozgás törvényei” 1666 óta érnek Newtonban. Pontosabban egy speciális mozgás, a forgó mozgás törvényei, amiben Huygens is olyan nagy eredményeket ért el. A Hold és a bolygók mozgásához, az eső kő mozgás-anomáliáihoz ezek a törvények elegendőek voltak. A „gravitás” mindig érdekelte Newtont, de másként, nem a „törvények”, hanem a képzelet, az ötlet, a fancy síkján – ahogy az 1675-ös hipotézisben leírta.78
Vagy ahogy alig egy éve, a Hooke-kal való levelezés során kiszámította egy „egyenletes gravitás” és egy érintőleges mozgás összetevődéséből kialakuló mozgás pályáját. Ott is egy centrumot került meg a két mozgás összetevődésének a hatására a mozgó test. – De nem ilyen bolond-hirtelen, mint Flamsteed kívánja. Lehet az üstökös pályáját számítani, neki van is erre módszere, s a számítások azt mutatják, hogy az üstökösnek – a decemberi üstököst érti alatta – dec. 3-án kellett metszeni az ekliptikát. Hogy milyen távolságban, azt megfigyelések hiányában nem tudja pontosan megmondani. Mindenesetre jóval túl lehetett a Napon.79 – De ha a decemberi üstökös dec. elején túl volt a Napon, akkor a decemberi és novemberi üstökösök aligha lehetnek azonosak.80
Ha ugyanis a második, a decemberi üstökös pályájából extrapoláljuk az első, a novemberi üstökös pályáját, ez semmiképpen sem vág a novemberi üstökös megfigyelt adataival. Számításai szerint a decemberi üstökös dec. 3-án metszette az ekliptikát, s ekkor a Föld – Nap távolság felével volt a Napon túl, s nem mozgott lényegesen sebesebben, mint később, már megfigyelhető szakaszában. Flamsteed hipotéziséből azonban az üstökös napközelére túlságosan nagy sebesség következne.
Ez pontatlan, rövid parafrázisa a meglehetősen bonyolult stereoastronomiai fejtegetéseknek, de gondos tanulmányozásukból is csak ez derül ki: akármilyen módszere volt is akkor Newtonnak az üstököspálya számítására, az a módszer nem az inverz négyzetestörvény és a centrifugális erőtörvény kombinációján alapult. Akkor ugyanis nem akadt volna fenn a Flamsteed hipotézise által megkövetelt nagy napközelbeni sebességen.
Newton nem lehetett túlságosan elégedetlen az üstökös pályájára végzett számításaival. Ugyanis a levél kéziratából a következő, el nem küldött részt közlik a kiadók:
„Hogy az üstökös a Napon túl járt, a magam részéről meglehetősen biztosnak látom, nemcsak azért, mert úgy tűnik, hogy a dolgok természete ellen van az az üstökösöknél, hogy úgy megforduljanak, mint az Ön hipotézise megkívánja, hanem azért is, mert úgy gondolom, hogy van egy módszerem az üstökös útjának (bármilyen vonal legyen az) a meghatározására, amely csaknem olyan pontos, mint amivel a bolygók pályáit határozzák meg, feltéve, hogy nagyon pontosan végzett, megfelelő megfigyelések állanak rendelkezésre. Ezért érdekelt az üstökös helyének a megfigyelése február végén és március elején…”81
Valóban, márc. 9-ig követi nagy érdeklődéssel és pontossággal. De mikor évekkel később megtalálja az üstökös mozgásának törvényét, akkor már nem lesz szüksége a sok pontos megfigyelésre: Flamsteed pár adatából meghatározza a pályát.
Az 1680–81-es üstökös kétségkívül felkeltette Newton érdeklődését az égi mozgások iránt. Az 1682 augusztusában megjelent üstököst is gondosan követte, s Flamsteeddel és más tisztelőivel is figyeltette.
A 80-as évek elejére esik Thomas Burnettel, a londoni Charterhouse főnökével való teológiai levélváltása is a világ szerkezetéről és természetéről.
Burnet többek között megkérdezte, mi a véleménye Newtonnak a Föld alakjáról: gömb-e az, vagy ovális? A válasz – indoklása miatt – meglehetősen érdekes:
„Nagyon hajlom afelé a föltevés felé – írja Newton –, hogy gömb alakú vagy enyhén ovális. És legfőbb érvem e vélemény mellett a bolygókról vett analógia. Amennyire teleszkóppal megítélhetők, mind kereknek látszanak. Ha napi mozgásuk oválissá tenné őket, a Jupitert sokkal oválisabbá tenné a maga mozgása, lévén egyenlítőjén a napi mozgása által okozott vis centrifuga 20 vagy 30-szor nagyobb, mint a Föld napi mozgása által okozott vis centrifuga a mi egyenlítőnkön.”82
Newton figyelme a 80-as évek elején, úgy látszik, több oldalról is a centrifugális erő felé fordul.
A levél további része hosszú teológiai fejtegetés a Genezis értelmezéséről.
„Ami Mózest illeti, nem hiszem, hogy teremtés-leírása philosophicus vagy kitalált lenne (philosophical or feigned), hanem hogy a valóságokat írja le mesterségesen a köznép értelméhez adaptált nyelven.”83
– foglalja össze több oldalra terjedő egzegézisét.
Sajnos, a Levelezés kiadói Newton óriási teológiai munkásságából csak nagyon keveset közölnek – a kiadás láthatóan a „pozitivista” Newtont szeretné feltámasztani – annyi azonban valószínűnek tűnik, hogy Newton kozmológiai érdeklődése nem teljesen „philosophicus” indítású. És nem is új: a 70-es évek nagy éterhipotézisei is ennek a szolgálatában állottak. Most azonban ez a kozmológiai érdeklődés egyre inkább mozgások és erők játékára koncentrálódik, mozgásokra és erőkre, amiket matematikai törvények uralnak.
A 70-es évek bontakoztatták ki Newtonban a nagy experimentátort, a spekulatív experimentális művészet egyik nagy megalapozóját. A 80-as évek Newtona szabja meg a természet matematikai törvényeit. Próféta lesz, egy egész elkövetkező kor prófétája, akit csak azért nem imádtak, mert a XVIII. és XIX. században ez már nem divat. A 80-as évek Newtona lesz az új civilizáció „Mózes”-e, s „tíz parancsolat”-a: a Principia három könyve. Leginkább a harmadik.
Ezt a könyvet fejezi be legkésőbb. 1684-től kezdve özönlenek a bolygórendszerre és az állócsillagok helyére vonatkozó kérdések Flamsteedhez. Alig győzi a megválaszolásukat.
Különösen a Jupiter-rendszer és a Szaturnusz érdekli Newtont. 1684. dec. 30-án izgatott hangú levél a Jupiter és Szaturnusz pályájáról:
„A Szaturnusz pályáját Kepler túl kicsinek definiálja a sesquialteratus arányhoz. Ez a bolygó, ahányszor csak conjunctióban van a Jupiterrel (a Jupiter reá való hatása miatt) túl kell fusson a pályáján egy vagy két fél-Napátmérővel, vagy még többel is, és mozgása csaknem egész többi részén ennyivel vagy még többel rajta belül kell legyen. Talán ez lehet az oka, hogy Kepler túl kicsinek definiálja. De én szeretném tudni, nem figyelte-é Ön meg, hogy a Szaturnusz Jupiterrel való conjunctiója idején jelentősen eltér Kepler tábláitól?”84
Flamsteed már január 5-én küldi a kért adatokat. Figyelemre méltó, hogy a korabeli Anglia legnagyobb asztronómusa, aki hallotta a Royal Societyben Halley beszámolóját Newtonnál tett látogatásáról, s talán már a Paget-levelet is látta – ha ugyan, mint előző levelében írta, „közös barátunk, Mr. Hooke és a többi városi”85 kielégítette már kíváncsiságát – Flamsteed, aki az elmúlt években Newton egyik legközelebbi munkatársa volt, milyen kevéssé él a Mester új gondolatvilágában.
„Hogy őszinte legyek – írja – alig hiszem, hogy valami befolyásuk lenne egymásra, mert a két bolygónak ebben a helyzetben az egymástól való távola csaknem négyszerese a földpályának (orbis annuus), úgyhogy ilyen képlékeny (yeilding) anyagban, mint a mi éterünk, nem tudom elképzelni, hogy egyik bolygó másikra való bármilyen impressziója is zavarhatná a másik mozgását.”86
Egyáltalán nem valószínű, hogy a bolygóknak valami hatása is lenne egymásra ilyen nagy távolból a Naphoz képest, amelyik
„a legnagyobb és leghatékonyabb mágnese rendszerünknek”.”
S most ő is tapasztalatra hivatkozik, mint pár évvel ezelőtti mágnes-vitájukban Newton: a legnagyobb eddig talált mágnes sem hatott 100 yardnál messzebb…87
De Newtont már nem érdeklik a „mágneses” tapasztalatok. Már jan. 12-én újra kérdez, a Szaturnusz-rendszer méretei érdeklik. – És nagy megkönnyebbüléssel veszi a Jupiter-Szaturnusz conjunctiójáról szóló értesítést:
„Kepler Jupiter és Szaturnusz tábláinak a hibáira vonatkozó információi számos gondtól szabadítottak meg. Már azt hittem, valami előttem ismeretlen ok lehet, ami megzavarhatja a Sesquialternatus proportiót… A legutóbbi levelemben végeztem egy becslést (allowance) a Jupiter és Szaturnusz egymástól való távolságára azon az alapon, hogy a távolság négyzetével fordított arányban csökken a virtusuk (virtue). De ott csak találomra beszéltem, nem ismerve virtusukat addig, amíg meg nem kaptam az Ön Jupiterre vonatkozó adatait, amikből megértettem, hogy virtusa kisebb, mint gondoltam…”88
A továbbiakban megköszöni, hogy átszámolja számára a francia üstökös megfigyeléseket:
„Szándékomban van az 1664 & 1680-as üstökösök által leírt vonalakat (lines) a bolygók mozgásánál megfigyelt elvek szerint leírni…”89
Ez sem lesz könnyű munka. Láttuk már, hogy azt mondja róla, pár hónap kemény számolást jelentett 1685 őszén… De amikor sikerült, akkor a nyert eredmények alapján az előző könyvek propozícióin is végzett némi javítást…
Amikor készen lett az üstökös-pálya bolygómozgás-törvényei szerint történő számolásával, akkor –
„…aláindula Mózes az hegyről, és az bizonyság tételének két táblái valának az ő kezében, mely tábláknak mind a két része megíratott vala, mind egyfelől, mind másfelől.
Az táblák penig Isten kezének csinálmányai valónak, az írás is Isten írása vala, mellyet kimetszett vala.”90
Nem volt-e valóban „bálványimádás” ezzel a művel szemben mindenféle prioritás-követelés? Isaac Newtonnak volt igaza, még akkor is, ha az inverz négyzetes törvény és az általános gravitáció ötlete a Robert Hooke állandóan matató agyában született is meg először.
S talán éppen az háborította fel annyira Newtont, hogy Hooke, akit ő semmiképpen sem tartott méltó ellenfélnek, lép fel ilyen követelésekkel.
Newton szeme előtt más, nagyobb, méltóságteljesebb ellenfél lebegett. Olyan, aki törvényt adott annak a világnak, amiben Newton felnőtt, s akinek nagyobb hatása volt Newton fejlődésére, mint hisztoriográfusai, s talán ő maga is, gondolták. Egy „igazi” ellenfél, s nem egy londoni „experimental” filozófus. Aki teremtett egy matematikai világmindenséget, aminél most Newton biztosabbat és „matematikaibbat” hozott létre.
Akit ő a matematikában szinte még gyermekkorában túlszárnyalt, akinek az optikáját egy évtized kemény küzdelmei árán egy mérhetetlenül „színesebbel” váltotta fel, s akinek a „világát” egy fél évtized hatalmas munkájával, a Hooke, Halley, Flamsteed, Huygens, az 1860-as üstökös és „az Isten” segítségével egy pontosabb világgal váltotta fel.
Nem Hooke volt a Principia-vitában Newton igazi ellenfele, hanem Descartes.






