Az Elemek
„ἀγεωμέτρητος μηδεὶς εἰσίτω”
„Ne lépjen be senki, aki nem ismeri a geometriát!”
Tartalom
Az Elemek
Bolyai János jegyzeteiből
Bolyai Farkas kolozsvári professzora – Méhes György
Méhes György – A. G. Kästner
Bolyai Farkas – Sipos Pál
Bolyai Farkas tanulmányai Göttingában, A. G. Kästner professzor keze alatt
Bolyai Farkas göttingeni „pipacimborái”
Heinrich Wilhelm Brandes (1777–1834)
Johann Joseph Anton Ide (1775–1806)
Johann Friedrich Benzenberg (1777–1846)
Újból otthon
Magyar Euklidész-fordítás a Bolyaiak hagyatékában
Az eddig megjelent magyar nyelvű Euklidész-fordítások
A különféle fordításváltozatok összehasonlítása
Bolyai János kézirathagyatékához tartozó 1554 jelzetű magyar nyelvű irat
Euklides elemei, XV könyv (Brassai Sámuel fordítása)
Euklidesz első hat könyve (Baumgartner Alajos fordítása)
Euklidész: Elemek (Mayer Gyula fordítása)
Észrevételek
Utószó
„ἀγεωμέτρητος μηδεὶς εἰσίτω”
„Ne lépjen be senki, aki nem ismeri a geometriát!”
Platón akadémiájának felirata rávilágít arra, hogy az ókor embere milyen jelentőséget tulajdonított a geometriának. Meghatározó szerepe volt világképében, és legfontosabb eszköze volt méréseiben, a napi gazdálkodó, építő és egyéb gyakorlati munkája során. Ezen tudomány alaptételeit – melyek felgyűltek az idők folyamán – Euklidész rögzítette Elemek című munkájában, amely a Biblia után a legtöbb nyelvre lefordított művek közé tartozik. Több mint két évezredig volt a gyakorlati tudományok legfontosabb segédeszköze.
Az Elemek a matematikai princípiumokkal kezdődik, melyeket Euklidész három csoportra osztott fel:
A definíciók a felhasznált kulcsfogalmakat magyarázták (pl. „Pont: az, aminek nincs része.”). A posztulátumok a megkövetelt kiindulási elveket sorolják. (pl. Követeltessék meg, hogy minden pontból minden ponthoz legyen egyenes húzható.) A princípiumok harmadik csoportja: az axiómák.
Az axióma olyan kiindulási feltételt jelent az érvelések során, amit adottnak veszünk. Olyan megállapított tény, alapigazság, amelynek igazságtartalma nem kérdőjelezhető meg (pl. „Ha egyenlőkhöz egyenlőket adunk hozzá, az összegek egyenlők.”). Egy axiómarendszerben az egyes axiómáknak egymástól függetleneknek kell lenniük (egyik sem vezethető le a többiből), míg az axiómarendszerre épült elméletnek ellentmondásmentesnek kell lenni (nem tartalmazhat egyszerre igazolható és cáfolható kijelentéseket).(1)
Az Elemekben az 5. posztulátum – későbbi kiadásában 11. axióma – a párhuzamossági axióma, amely a sík egyeneseinek egyik tulajdonságát kimondó feltételezés. Egyik változata:
„a párhuzamos egyenesek azok az egy és ugyanazon síkban fekvő egyenesek, amelyek mindkét irányban határtalanul megnyújtva nem metszik egymást.”
Már Euklidész első kommentátorainak feltűnt, hogy a párhuzamosok axiómájában a „metszés” tapasztalattal nem ellenőrizhető, tehát a XI. posztulátum nem magától értetődő, nem olyan igazság, amit bizonyítás nélkül el lehetne fogadni, s ezért megkísérelték levezetni. Próbálkoztak azzal is, hogy a posztulátumot, vagy a párhuzamosok euklideszi definícióját más fogalmazásokkal helyettesítsék. A sikertelen próbálkozásokat több mint két évezreden át újabbak követték, ám az alternatív definíciók és axiómák nem vezettek eredményre. Ezek a kutatások egészen a XIX. századig sikertelenül folytak. Minden magát matematikusnak tartó személy megpróbálkozott a feladat megoldásával, köztük Bolyai Farkas is, hiszen ő már fiatal kolozsvári diákként találkozhatott a több ezer éves dilemmával.
Végül a kérdésre megnyugtató megoldást Bolyai János talált, aki hihetetlen merészséggel továbblépett apja szövegértelmező kísérletein: egyszerűen függetlenítette a geometriát a párhuzamosok axiómájától és felépítette a sík és a tér V. posztulátumtól (vagy XI. axiómától) független nemeuklideszi, vagyis abszolút geometriáját. Ezt a címet adta geometriai munkájának:
„Appendix. Scientiam Spatii absolute veram exhibens: a veritate aut
falsitate Axiomatis XI. Euclidei (a priori haud unquam decidenda)
independentem”
[„Függelék. A Tér abszolút igaz Tudománya, a XI. Euklidész-féle axióma (a priori soha el nem dönthető) helyes, vagy téves voltától független tárgyalásban”]
Műve – az Appendix – felkerült a Világemlékezet listára1 (erről részletesebben itt olvashatunk).
És most tekintsük át azt az utat, amit Bolyai János számára a nagy elődök kiköveztek ahhoz, hogy az övé legyen a siker, az elismerés.

János maga több feljegyzésében utal arra, hogy matematikusi érdeklődésének mi volt a forrása. Idézünk néhány részletet idevágó feljegyzéseiből:
„Atyám oltotta belém azt a múlhatatlan szenvedélyt, hogy megtisztítsam a geometriát a párhuzamosok zavaros elméletétől. Ha atyám költői képekkel, szenvedéllyel és tudománytörténeti háttérrel nem plántálja belém ennek fontosságát, akkor az én roppant fontos Tér Tudományom sem születik meg.”
„Most persze hiába is hánytorgatnám fel Atyámnak, hogy azt ígérte, aki megoldja a párhuzamosok problémáját, az akkora gyémántot érdemel, mint a Föld.”2
Igyekszünk kimutatni, hogy Bolyai Farkasnak az euklideszi geometria, ezen belül a párhuzamosok iránti érdeklődése Göttingából – előbb közvetve Méhes Györgyön át, majd közvetlenül Göttingában A. G. Kästner professzortól – eredeztethető. Bolyai kolozsvári matematika professzora Méhes György ugyanis Göttingában A. G. Kästner professzortól – a közismert Euklidész kutatótól – tanult matematikát. Később maga Bolyai is külföldi tanulmányait Göttingában folytatta, és a matematikát immáron ő is közvetlenül A. G. Kästner professzortól hallgatta. Az apa is továbbadta fiának és tanítványainak azokat a geometriai ismereteket, amik az ő korában foglalkoztatták a világ matematikusait. Tekintsük át az erre utaló legközvetlenebb forrásokat. Önéletrajzi, kéziratos feljegyzésekre, levelezésre, valamint egyéb kordokumentumokra hivatkozunk. Kezdjük mindjárt Bolyai János kézirataiban olvasható idevágó jegyzetrészletekkel:
„Az általam szeretett Atyámtól kell kezdenem életem summázatát. Ő is kiváló matematikus volt. Már gyermekkorában csodagyerek, de tanítói hóhérai lettek, mert nem tudták kellő tapintattal kezelni atyám sokféle tehetségét. Nem a jó irányba vezették szellemi fejlődését, hanem a magamutogatás, pillanatnyi sikerek csalfa csillogásába. Ez aztán egész életét és tevékenységét meghatározta.
Atyámnak a szerencsétlen életében egy kis szerencse, hogy Fehér megye szigorú és konok főispánja, báró id. Kemény Simon a családjába vette, és fia tanulótársaként kiküldte Göttingenbe. Ott, Göttingenben látta meg aztán Atyám, hogy mi is az igazi tudomány, és hogyan is kell ahhoz közeledni. Talán akkor ott voltak Európa legkiválóbb tudósai. Az általam igen tisztelt Atyám ott ismerkedett meg Gauss-szal, és tőle tanulta meg a mély elmélkedés és az alapos matematikai vizsgálódás varázsát. Ott értette meg, hogy a tudomány nem a pillanatnyi fellángolásokból áll, hanem a hosszú-hosszú előkészületekből és alapos tani vizsgálatokból. […] a matézis tiszta szeretetét áldott emlékű Atyám plántálta belém. Igaz, hajlamom is volt rá, de Atyám ügyes adagolása és kellő időben történt, szenvedélyes magyarázatai által jutottam el oda, ahol állok, vagyis sikerült megreformálnom az egész tant. Új alapra helyeztem a tér tudományát, és az eljövendő nemzedék igazolni fogja tanom helyességét.…
[…] nagyon megszerettem a matematikát és minden örömöm abban telt, ha feladatokat oldhattam meg. Szerettem matematikát olvasni, ebben nagy szerepe volt szépelméjű Vajda Dánielnek, akit Atyám mellém fogadott tanítónak.
Én 9 éves koromban kezdettem űr-tant tanulni Euklid szerént, s meglehetős levén sikere: nem is igen későn.3
A matematikára főleg Atyám tanított, de azért megbeszéltük az elméleteket eleinte Vajdával, aztán én hamar túlléptem Vajda matematikai tudásán, és akkor már csak Atyám tudott nekem segíteni. Euklidesz 15 könyvének végigolvasásában még segített Vajda, főleg a latin szöveg fordításában, de aztán az integrál- és differenciálszámításban már csak Atyám tudott irányítani. Nagyon gyorsan haladtam a tanulásban, az igazat megvallva, a többi tárgyat erősen untam. Bár elismerem, hogy fölöttébb fontos a történelemtan, a bölcselet, a teológia, de abban egyedül is lehet haladni, ha az ember elolvas mindent.
Én is voltam olyan okos, mint Atyám gyermekkorában, de Atyám nem engedte, hogy bohócot csináljanak belőlem, mint ahogy Vele tették a nagyenyedi tanárai, akiket Ő maga is sokszor a hóhérainak nevezett. Lassan adagolta belém a tudományokat, mértékkel és kellő türelemmel. Azt tartotta, hogy legyen szolid az alapozás, akkor akármilyen építmény majd biztonságosan megáll rajta. […]
Atyám szerette volna, ha Gaussnál folytatom majd a továbbtanulást, ezért igen különösen megkövetelte, hogy tökéletesen ismerjem a németet. Az igazsághoz tartozik, hogy a Bécsi Hadmérnöki Egyetem elvégzése után már jobban tudtam németül, mint magyarul, főleg ami a tudományok megértését illeti. Szóval Atyám Gausshoz akart küldeni, és ezt sokszor emlegette is nekem. Egy hiú reményt is belém plántált, hogy nekem csak Gaussnál szabad matematikát tanulnom, ha azt akarom, hogy jó matematikus váljék belőlem. Igen ám, de éppen mire 12–14 éves lettem, megszakadt Atyám és Gauss levelezése. Éppen amikor befejeztem a négyéves tanulmányomat, akkorra lett teljesen reménytelen a Gaussnál való továbbtanulásom….”4
A további mondanivalónk számára a visszaemlékezésekből három gondolat rendkívül fontos: mikor kezdett Bolyai János az Euklidésszel foglalkozni, hány könyvét ismerte, valamint Vajda Dániel Euklidész-fordítói és magyarázó szerepe. Minden jel szerint Bolyai János egy latin nyelvű Elemek kötetből tanulta Euklidész geometriáját, saját bevallása szerint 9 évesen, ami megfelel a mai 3-ik elemi osztálynak, és Vajda Dániel, a házitanítója, előbb latin nyelvről magyarra fordította, majd a megértésben is segédkezett. Végigolvasta mind a XV. könyvet.(2)
Vajda Dániel – János házitanítója – Bolyai Farkastól tanult a kollégiumban, és azt is tudjuk, hogy a kollégiumi matematika oktatásban Euklidész geometriája kiemelt helyet foglalt el, amint ezt Bolyai Farkas egyik – feletteseinek írt – jelentése tanúsítja:
„Mathesisbe további rendelésig Kaestnert […] követem, s azon kívül a mathesis tanítását az eredeti Euclidesnek (a Föld fő mathematicussai tanítójának) hat könyvén kezdeni tapasztaltam legfontosabbnak.”5
Léczfalvi Vajda Dániel (1793–1860) Bolyai Farkas egyik legtehetségesebb tanítványa volt. Korán árvaságra jutott, nélkülözések és küzdések között tanult, 1814-ben a bécsi egyetemre ment, később Erdély híres borásza lett. Bolyai őt választotta fia mellé házitanítónak, az árva fiú szinte családtagként élt Bolyai házában. Bolyai Farkas atyai gondoskodással egyengette Vajda pályáját. Figyelemreméltó az az üzenet, amivel külföldi tanulmányútjára bocsátja tehetséges tanítványát. Íme a közel 200 éves emléklap:
„Minden ember eggy summa a’ (+) ból és (–) ból, vigyázzon! ne hogy a’ (+) ra, mellyel a’ jóknak állandó szeretetére praenumeralta, a’ növő (–) árnyékot vessen. Ha a’ (+) növése a’ (–) táplálása lenne, inkább a’ (–) apadásával igyekezzék nőni; inkább beteges maradnék, ha tudnám, hogy a’ test egészségit a’ lélekből kell fizetni.
Az élet maga is eggy algebrai summa, mindenik korba (+) és (–) ból, mellynek valorának értékének nőni kellene, ha az ifjúság arithmeticaja hibáit a’ felső korba által nem vinnök.
A’ hamar elvirágzó rósákon túl nézve őszre gyümölcsöst plántáljon, a vénség leginkább az élet ideje, addig inkább készült.
Mi szebb mint eggy fejér haju öreg, mikor az ideje méllységéből lefutott pályajára örömmel néz vissza, s az örök élet hajnala mosolyog reá.
Gondoljon ide az ifjúság szédítő kísértései között. Főként emlékezzék meg illendő távolságba maradni a’ szép nemre nézve, tsudálatos ópium ez, melly az ifjúság reggeli idejét elaltatja, s a később korok boldogságát hiába való álmokkal fizeti. Hogy pedig vén lehessen, legyen mértékletes mindenben, a’ munkában s nyugodalomban is – a’ pipában is.
N.B. Különösön amellyel való mértékletes élés is mértékletesség. A szemire vigyázzon, minthogy gyenge. A szállása nedves ne legyen, a napot ne engedje reggel, hogy bérohanjon az elszokott szemire, szembe ne verődjék a’ nap fényes falról vissza, a szürkületben ne irjon, olvasson.
Irta emlékezetül … barátja
Bolyai Farkas”6
És most vizsgáljuk meg az apa – Bolyai Farkas – kapcsolódását Euklidész geometriájához, valamint azt, hogy mi volt az útja az euklideszi elméletek áttételének térben és időben Erdély–Göttingen–Erdély között?
Igencsak érdekes a kialakult euklideszi „ALMA ÉS FÁJA” struktúra: Bolyai János–Vajda Dániel–Bolyai Farkas–Méhes György–A. G. Kästner, végül közvetlenül Bolyai Farkas–A. G. Kästner és a göttingeni kutatóegyetem diáksága. De előbb nézzük meg milyen szellemi képességek birtokában fordult Bolyai Farkas érdeklődése a matematika és tanárai felé? Önéletrajzában részletes választ kapunk ezekre a kérdésekre. Bolyai Farkas ténylegesen csodagyerekként került előbb az nagyenyedi, majd a kolozsvári református kollégiumba. Ő maga így vall saját képességeiről, tanárairól:
„Radix quadratát, cubicát [négyzet-, köbgyök] húztam eszemben hiba nélkül tizennégy számból is, a végén mégtöbb számot kérve, szólottak hozzám, feleltem – elküldöttek, s helyemre menve vissza a táblán képzelt írást ott találtam ahol félbeszakadt, s mind a táblán képzelve folytattam de az okát nem tudtam, még azt sem, hogy okát kell tudni. […] Csakugyan ezen hírem következéséül, mikor a német classisból rhetor lettem, […] Kolozsvárra, a híres theológiae professor Szathmári (Pap) Mihály házához mentünk lakni és ottan több professorokat járván, végre négy napi censurát adtunk a nagy auditoriumban. A mathesist a mostani (1840) derék professor Méhes Sámuel derék atyjától (M[éhes] Györgytől) hallgattuk…”7
Oktatástörténeti különlegességnek számít Bolyai 1792-es év végi vizsgája is, amelyet a Kolozsváron ülésező Diéta előtt tett két tanulótársával együtt. Az esemény oly mértékben jelentett szenzációt a maga korában is, hogy a bécsi Magyar Hírmondó is megírta. Érdemes végigolvasnunk a több mint 220 éves újságcikket:
„Kolozsvárról, Nov. 1. napján. A Reformátusoknak itt lévő Kollégyiomában ritka jelességű Examen tartaték a közelébb lefolyt Október hónapnak 2-dik, 3-dik, 4-dik és 6-dik napjain. Tetsztvén ti. Mélt. Báró és Fő-Ispány Kemény Zsigmond [Simon] Úr Ő excell.-ának, hogy maga nevét viselő, nagyraszületett kedves úrfia az egész Diéta előtt adná próbáit a nagyobb tudományokban tett előmenetelének, megkérte az Ország Rendjeit, hogy a feljebb említett napokra ne terheltetnének megjelenni a Ref. Kollégyiom nagyobbik Auditóriumában. Megjelentek minden valláskülönbség nélkül, mert kívántak részt venni egy nagy hazafi társoknak atyai s egyszersmind hazafiúi örömében, s ösztönt adni az ifjú hazafinak maga további tökéletesítésére, melynél fogva ti. belőle is egy derék oszlop embere válhasson a Hazának; hogy a Haza érdemes lányai új bizonyságát adhassák ugyanazon közönséges, jó lélektől (Esprit public) való vezéreltetéseknek, mely lelkesíti a hazafiakat: megjelentek ők is az ifjú báró felől való nagyreménység nyomós voltának édes tapasztalására. Első napon nagyérdemű Professzor Tiszt[eletes] Szatmári Pap Mihály úr examinálta az egész Theológiából az ifjú bárót és két tanulótársait úgymint: Bolyai Farkas és Szatmári Pap Zsigmond nemes ifjakat. Az utóbb említett tulajdon fia professzor úrnak. Három órákig tartott a vizsgálás, deák nyelven. ój készséggel és értelemmel feleltek mind a három ifjak, kivált a báró úrfi, hogy még a nagy gróf Teleki József úr is azon szíves örömét jelentette. Másodnapon hasonló fényes gyülekezetben mind a 4 vallást tartó uraságoknak említett Tiszt. Szatmári Pap Mihály úr volt a kérdező, akinek házánál lakik ugyancsak a báró úrfi, már két esztendőtől fogva, öccsével és különös tanítójukkal együtt. Ez nap is deák nyelven kezdődött az examen a római régiségekből (Antiquitásokból), hanem a méltóságos asszonyságok kedvekért csakhamar magyar nyelvvel cserélődött fel a deák s azon folyt egész végig, mindössze 4 órákig. Sok uraságok azt vallották, hogy ennél szebb exament nem hallottak. Harmadik napon a philosophiae professzor T. Méhes György úr examinálta a 3 ifjúkat a mathésisnek némely részeiből. Ottan-ottan kérdéseket tett fel gróf Teleki József belsőtanácsos úr is és mind Ö-Excell.-jától mind másoktól különös dicséretet érdemlettek a remekelők. Negyedik napon, éppen azon úri hallgatók előtt, kik már három napokon tisztelték volt meg jelenlétekkel a nagy Ref. Kollégyiom nagy Auditóriumát, tulajdon tanítójok az ifjaknak T[ekintetes] Incze István úr fejezte bé az exament, mely volt ez nap a logikából és metafizikából. Ezúttal sokan tettek fel kérdéseket az uraságok közül. Vége lévén a próbatételeknek, mind különösen mind átaljában örömmel magasztalta az egész fényes gyülekezet mind a tanítóknak, mind a tanulóknak szíves törekedéseket. Még egy esztendőt fog tanulni a hazában ifjú B[áró] Kemény Simon ŐN[agysága] valamint tanulótársai is és ezután külső országokra igyekeznek tudományok öregbítése végett. Idejekre nézve mindhárman a l6-ik esztendő körül járnak.”8
Vajon képes lenne-e ma egy gimnazista diák erre a 220 évvel ezelőtti szellemi bravúrra, hogy az országgyűlés előtt levizsgázzon matematikából, teológiából, történelemből, logikából, metafizikából váltogatva a nyelveket magyar és latin között, ugyanakkor, vállalva a hallgatóság sorából elhangzó kérdéseket is?
Mit is tudtunk meg az újsághírből, ami visszakapcsol Euklidészhez? Azt, hogy „Harmadik napon a philosophiae professzor T. Méhes György úr examinálta a 3 ifjúkat a mathésisnek némely részeiből.” Vagyis Kolozsváron Méhes professzor oktatta Bolyainak a matematikát, akivel személyesebb jó viszonyban volt. Külföldre indulása előtt ugyanis Méhes – a kor szokásainak megfelelően – atyai hangú emléksorokat ír Bolyainak:
„Omne tulit punctum miscuit utile dulci.
Memoriae causa ad posuit
Georgius Méhes
in Collegio Reform. Claudiopolitano Philos. et Mathes.
L[aureatus] Professor
Claudiopoli. Die 4-a September. 1795”
[„Általános tetszést az arat, aki a hasznosat a kellemessel elegyítette.
Emlékül ideírta
Méhes György
a kolozsvári Ref. Kollégiumban filozófia és a mathézis
laureatus professzora.
Kolozsvárott, 1795. szeptember 4. napján”]9
Nem tévedünk, ha azt állítjuk, hogy Bolyai Farkasnak a matematika iránti elkötelezettségében Méhes Györgynek komoly szerepe volt. Méhes Göttingában a kor híres Euklidész kutatójától – Kästnertől – tanult matematikát. Kolozsvári professzorként bizonyára ő is tovább adta diákjainak a Kästnertől megismert és a kor matematikusait izgató feladatokat, így Euklidész axiómájának bizonyítása iránti érdeklődést is. Azt is okkal feltételezhetjük, Méhes igyekezett meghonosítani a göttingeni kutatóegyetemen kötelező professzor–diák közös gondolkodás módszerét is. A matematika zseni Bolyai esetében minden bizonnyal alkalmazta. Erre Oláh-Gál Róbert Bolyai-kutató írása is utal:
„Véleményem szerint Bolyai Farkas matematikusi tudását Méhes György, a kolozsvári Református Kollégium professzora alapozta meg. Erről csak akkor győződtem meg igazán, amikor belepillanthattam Méhes György kézzel írt Geometria tankönyvébe. Ez a mű egy mai geometria tankönyvnek is megfelelne, de lehet, hogy jobb, mint a mai tankönyvek. (Lásd a mellékelt ábrát.)”
Ha vetünk egy pillantást Méhes György tankönyvébe, rábukkanunk elméletünk bizonyítására, a párhuzamosok tárgyalására.10

Bolyai felnőtt korában is baráti viszonyban állt hajdani professzorával. Amikor Méhes fia, Sámuel Göttingába készült egyetemre, Bolyai ajánlólevelet küldött Gausshoz, és pártfogását kérte az ifjú Méhes számára. A két Bolyai világképét, természettudományos szemléletét, dialektikus gondolkodásmódját, a matematika iránti szenvedélyes elkötelezettségüket és az eredményt – a Bolyai-geometria alapköveit – joggal származtathatjuk Méhes Györgytől.
Most pedig vizsgáljuk meg milyen matematikai ismeretek birtokában kezdte meg Kolozsváron – külföldi tanulmányútja után – Méhes György (1746–1809) a tanári munkát? Tudjuk, hogy felsőbb tanulmányait 1773-tól a göttingeni és utrechti egyetemeken végezte, ahonnan 1775-ben tért haza. Göttingában bizonyára az akkor 54 éves Kästner tanítványa volt, és matematikai felkészülésére hatottak Kästnernek az Elemekkel kapcsolatos kutatási eredményei. (Kästner tudománytörténeti jelentőségére a továbbiakban visszatérünk)
A göttingeni Georgia-Augusta, a világ legelső úgynevezett kutatóegyeteme volt. Az egyetemi program egyik új vonása volt, hogy a professzoroknak egyaránt kellett oktatói és tudományos kutatói tevékenységet folytatni. A még ki nem forrott eredményekről is rendszeresen be kellett számolniuk az oktatói kar és a diákság előtt. A. G. Kästner (1719–1800) professzorról internetes források azt írják, hogy
„főleg matematikatörténeti és összefoglaló műveket írt. Sokat foglalkozott Euklidész párhuzamossági axiómájával. Bolyai Farkas tanára volt, így minden bizonnyal hatást gyakorolt Bolyai Farkas, valamint közvetetten Bolyai János ilyen irányú munkásságára.”11
A Bolyaiak életrajzírója – Bedőházi – ezt írja Kästnerről:
„Kästner megszállottan vizsgálta Euklidész axiómáit. Kästnernek különben halhatatlan érdeme, hogy Klügellel (1739–1812)12 együtt kiadják a párhuzamosok elméletének történetét 1763-ban. Kästner körülbelül 7000 darab művet gyűjtött össze, a melyek majdnem teljesen tartalmazzák mindazt, a mit e kérdésről 1770-ig írtak.”13
Ez a kötet Méhes göttingeni tartózkodása alatt közkézen foroghatott, Kästner pedig minden bizonnyal diákjainak is továbbadta az euklideszi geometria kapcsán felmerült kérdéseket, kutatási eredményeket és bevonta őket is a paralellák axiómájának bizonyítási kísérleteibe. A több ezer tételes Euklidész bibliográfia összeállításában – ha hihetünk Bedőházi adatának – a diákok is kivehették a részüket.
Bolyait külföldre indulása előtt minden bizonnyal Méhes – egykori professzorához –, Kästnerhez irányította Göttingába. Kizártnak tartjuk, hogy pályaválasztási tanácstalanságában Méhes ne arra bátorította volna a matematika csodagyerekként számon tartott Bolyait, hogy Göttingába menjen. Itt az euklideszi geometriával kapcsolatos dilemmák vizsgálata intenzívebb lehetett, mint bárhol a világon.
De volt még egy híres matematikus kortársuk, aki hathatott Bolyai ingadozó egyetemválasztási döntésére. Ugyanis élénk volt az érdeklődése a bécsi katonai akadémia iránt is. Beiratkozása előtt felkereste az akkor Teleki Sámuel erdélyi kancellár udvarában élő Sipos Pált, aki nem sokkal korább érkezett haza egyetemi tanulmányútjáról. Többek között Göttingában is tanult, az ő matematikatanára is A. G. Kästner volt, aki
„a későbbi évek során gyakran váltott levelet Sipossal. […] 1793-ban Sipos Pál Bécsbe került, itt Teleki Sámuel fia, Ferenc mellett nevelő. 1795-ben (frankfurti munkásságát jutalmazva) a Berlini Akadémia aranyéremben részesítette. Eredetileg 50 aranyat akartak neki adni, de a pénztár kedvezőtlen helyzete miatt végül aranyérmet kapott. 1700-tól 1854-ig Sipos az egyetlen, aki nem volt tagja a Berlini Akadémiának és értekezését mégis kiadták. Ez művének jelentőségét igazolja. Az akadémia történetében ő az egyedüli személy, aki pályázat nélkül nyerte el ezt a kitüntetést. Az aranyérmet és az elismerést azért kapta, mert megújította a matematikai szerkesztések módszerét. Ő vonalzón és körzőn kívül egy saját találmányt is használt, az izométert. Ez tulajdonképpen egy olyan eszköz, mint a szögmérő, csak az alapja nem kör, hanem egy csigavonal, amelyet később Sipos-görbének neveznek el.”14


Bolyai 1796 nyarán – ellentétben az eddigi életrajzírók adataival – Bécsben tartózkodott és találkozott Sipos Pállal és kis Teleki Ferenccel, akiktől egy-egy emléklapot kap:
„Emlékezz arra, amit Cicero művében Scipio mond magáról:
A bölcs soha kevésbé nem nyugodt, mint amikor nyugodt, és soha kevésbé nem magányos, mint amikor egyedül van.
Szeretném, ha ezt a barátságból
irt lemondatot barátsággal fogadnádSipos Pál sk.
Bécs, 1796. július 9.”15
Mindent kétséget kizáróan ezen találkozáskor szóba került Sipos matematikai eredménye, göttingeni tanulmányai és pályaválasztási tanácstalansága közepette minden bizonnyal Sipos arra ösztönözte Bolyait, hogy válassza Göttingent, ahol magas színvonalú matematika képzésben lehet része.
Életüknek később volt még egy „találkozása”. Az 1800-as évek elején, amikor a marosvásárhelyi kollégiumba matematika professzort kerestek, Sipos volt, akire a javaslattevő professzorok nagy része szavazott. Sipos azonban a papi pálya mellett döntött, így végül a második helyre került Bolyai nyerte el az állást.

Bolyai Farkas 1796 őszén végül ugyanarra a külföldi egyetemre iratkozott – a göttingai Georgia-Augustába –, ahol egykori kolozsvári tanára, Méhes is tanult és ahol A. G Kästner még mindig tanított. Bolyai önéletrajzában ezt írja:
„Göttingába mentünk, az holott is Kästner, Linchtenberg szenvedhettek, s megismerkedtem az akkor ott tanuló Gaussal, kivel máig is barátságban vagyok, noha távol attól, hogy vele mérkezzem; a legszerényebb s a legkevesebbet mutató; nem harmadnapig, mint Plátóval – évekig lehetett vele valaki a nélkül, hogy megtudja nagyságát – kár, hogy nem tudtam ezt a czimtelen sarkú, hallgató könyvet felnyitni, s olvasni; én se tudtam hogy milyen sokat tud, s ő is saját módomat látva igen sokat hitt rólam, s nem tudta, mely kevés vagyok – az igazi (nem könnyüszerüleg szinen járó) mathesisi szenvedelem s erkölcsi egyezés kötött egybe úgy, hogy többször gyalog utazva együtt, mindenik könyv maga tárgyáról gondolkodva órákig nem szólottunk.”16
A göttingeni Georgia-Augusta kutatóegyetemről Békés Vera A kutatóegyetem prototípusa: a XVIII. századi göttingeni egyetem című tanulmányában egyebek mellett ezt írja:
„A göttingai iskola tudósait, ([…] A. G. Kästner, K. F. Gauss, J. F. Blumenbach, A. […] vagy G. C. Lichtenberg nevét említenünk)17 egyszerre több, különböző tudománytörténeti kutatás is méltányolja, (matematika, fizika, botanika, zoológia, földrajz, régészet, antropológia, filológia, fiziológia, etnográfia, hermeneutika, jogtudomány, irodalomtörténet stb.) egymástól függetlenül, sőt, egymás eredményeiről mit sem tudva[…] A modern egyetemen is előfeltételezik a tanár tudományos kutatói munkáját – ez feltétele a kinevezésnek, […] de azt mintegy a szerződésbe foglalt kötelezettségein kívül, magánemberként, szabadidejében kell végeznie.
A kutatóegyetemen a tudományos kutatómunka, mint hivatásra való felkészítés az oktatási program szerves részét alkotja[…]
A göttingeni professzorok a diákjaikkal szoros közösségben élve intenzíven tanítottak és kutattak. A tanárok mindemellett nagyfokú szabadságot és jelentős állami támogatást kaptak tudományos vizsgálódásaikhoz. Viszont elvárták tőlük, hogy eredményeikről rendszeresen, nyilvános számot adjanak.”18
A professzorok tehát a mindenkori diákjaikat bevonták a kor nagy kérdéseit vizsgáló kutatásokba. Az akkor már 70 évén fölött járó Kästner sem tett bizonyára másképp. Nem véletlen, hogy Bolyai akkori diáktársai – a „pipacimborák” – közül világhírű matematikusok, csillagászok kerültek ki. C. F Gaussnak azaz a „princeps matematicorum”-nak az euklideszi geometria iránt érdeklődése közismert. További „pipacimborák” voltak olyan tudósok is, mint J. A. Ide, F. J. Benzenberg vagy H. W. Brandes.
De milyen baráti viszonyban volt Bolyai ezekkel a fiukkal? Milyen tudományos jelentőségük volt a maguk korában? Első kérdésünkre választ találunk azokban az emléklapokban, amit elválásukkor írtak Bolyainak.

Göttingeni tartózkodásának legszorosabb barátsága C. F. Gausshoz kötötte. Carl Friedrich Gauss (1777–1855) magasan kiemelkedő tehetségű tudós volt, a „matematika fejedelmé”-nek is nevezték. Bolyaival egész életükben – kisebb-nagyobb megszakításokkal – levelezésben álltak. Levelezésüket nyomtatásban is kiadták.19 Euler, Newton és Arkhimédész mellett Gausst tartják minden idők egyik legnagyobb matematikusának. Bolyai hazaindulása előtt – a kor szokása szerint – legjobb barátai emléksorokat írtak a peregrinációs útikönyvébe (Album amicorum; Stammbuch; Memory or friendship book). Bolyainak 85 ilyen lapja gyűlt össze, amit jelen cikk írója nyomtatásban is megjelentetett.20
Az itt idézett emléklapok olyan barátoktól származnak, akik valamennyien a tudománytörténet kimagasló személyiségei lettek. Azért tartottuk érdemesnek idézni ezeket a sorokat, hogy rávilágítsunk Bolyai szoros, bensőséges viszonyára ezekkel a fiatalokkal, akikkel bizonyára sok közös matematikai vitát folytattak le esténként borozgatás, vagy séta közben.
Csillagász, fizikus, természettudományos kutatásai révén a német tudománytörténet ismert alakja lett. Abban az évben, amikor Bolyainak az emléklapot írta nagy visszhangot keltett azzal a tudományos felismerésével, miszerint a hullócsillagok földön kívüli eredetűek. 1826-tól a Lipcsei egyetem fizikaprofesszora. Elsőként rajzolt szinoptikus térképet. Bolyai Farkas és Gauss levelezésében gyakran előfordul a neve igazolva barátságuk voltát. Ezt sugalmazza a Klopstock idézet is.
„Ich kann mir beim Abschiede nichts Bessers wünschen,
als daß Sie mich einst auch in Ihren frohen
Stunden, in den Wunsch
Klopstocks einschliessen:
Waret ihr auch bei uns, die ihr mich ferne liebt,
In des Vaterlands Schoß, einsam von mir verstreut,
die in seligen Stunden
Meine schuchende Seele fand;
O dann bauten wir hier, Hütten der Freundschaft uns!
Ewig wohnten wir hier, ewig! Der Schattenwald
Wandekt uns sich in Tempe
Jedes Thal in Elysium!
von Ihrem Sie sehr schatzenden Freunde
Heinrich Wielhelm Brandes.
Göttingen, 30. Novemb. 1798.“
[„Búcsúzáskor nem kívánhatok semmi jobbat magamnak,
mint hogy az Ön majdan, boldog óráiban belefoglaljon a
Klopstock szerinti kívánságba:
Lennétek ti is nálunk, mindazok kik távolról szerettek
a haza ölében magányosan szerteszét szóródva,
Akikre lelkes óráiban kereső lelkem rátalált,
Óh, akkor mi a barátság menedékét építhettük volna itt,
Itt élhettünk volna örökké, örökre!
Ez árnyékvilág számunkra Tempevé vált volna,
Minden völgy Elyseumm!Önt nagyrabecsülő barátjától
Heinrich Wilhelm BrandesGöttingen, 1798. November 30.”]
Gauss gyermekkori barátja, ugyanabból a városból, Braunschweigből származnak mindketten. A Bolyai–Gauss levelezésben egyik leggyakrabban emlegetett név. Az 1798–99-es év során Gauss már nem élt Göttingában. Bolyai rendszeresen beszámolt neki az ottani eseményekről:
„Idével együtt voltam néhányszor, világos fejű embernek találom, és nagyon közlékenynek saját dolgaiban; már bemutatott nékem egyet-mást, amit nyomtatásra előkészített, köztük a felsőbb kalkulust, amely (mint ő mondja) egynémely új felfedezést tartalmaz, igazán röviden és elegánsan előadva.”
„Ide jó mulatságot szerzett nekem, mert a geometrice akarta bebizonyítani az ördög képtelenségét azzal, hogy csupa befeléfordult szögből nem lehet sokszög, s így ennek megfelelően nem létezhetik minden ízében bűnös lény sem.”21
Idét 1803-tól meghívták a Moszkvai Egyetemre matematikatanárnak, tüdeje azonban nem bírta a hideg klímát, és 1806-ban tüdőbajban meghalt.
„Was den großen Ring bewohnet
Huldige der Sympathie!
Zu den Sternen leitet sie
Wo der Unbekannte thronet!
Zum Andenken an Ihren Freund
J. J. Anton Ide
Göttingen den 30ten Mai 1799“
[„Ami a nagy körön belül lakozik
Az hódoljon a rokonszenvnek!
Ez a csillagokig vezet,
Ahol az Ismeretlen trónol.Emlékeztetőül az Ön barátjára
J. J. Anton Ide
Göttingen, 1799. május 30.”]
Német matematikus, csillagász. 1798-ban H. W. Brandessel közösen bebizonyították a meteorok kozmikus eredetét. Bolyai gyakran emlegeti az ő nevét is a Gausshoz írt levelekben. Többször próbált egy-egy példányt Benzenbergnek is eljuttatni a kinyomtatott matematikai munkáiból.
„Berge trennen,Taler trennen
Angesicht von Angesicht
Aber Berg, und Taler trennen
Gleichgesinnte Seelen nicht.
Zum Andenken von Deinem Freunde
J. Fr. Benzenberg
von Schöller bei Düsseldorf
(Symb: Praeterea et censeo Cartaginem
esse delendam)“
[„Hegyek választhatnak, völgyek választhatnak el
Arcokat egymástól
De hegy és völgy elválasztani
Hasonlelkeket nem tud.Megemlékezésül barátodtól
Schölleri J. Fr. Benzenberg
Düsseldorfból(Figyelmeztetés: Továbbá úgy gondolom,
hogy Karthágót le kell rombolni.)”]
Az emlékezetes göttingeni évek után 1799 nyarán Bolyai gyalog indult haza Erdélybe. Elindulására így emlékezik önéletrajzában:
„Feljött a pénz, s leindultam gyalog. Az astronómia professor (aki Napóleonnal volt Austerlitznél s azután ingenieur Oberstere lett) s mások a szomszéd faluig kiértek gyalog; az elváláskor sírva mint a gyermek, akaratom ellen mentem vissza, míg erőt vettem magamon, az utolsó tetőről, az honnan még látszott Göttingen, még egyszer visszanéztem, megállva míg az örökre elválás homályában a Daguerrotyp megmaradott. De most is visszatekintek még egyszer:
Gauss Braunschweigból irt volt, hogy határozzak napot és helyet Göttingán kívül, a mikor és hol még egyszer találkozzunk; mindenkor pontosak, akkor is azon egy órában érkeztünk gyalog Clausthalba, ahonnan reggel egy tetőig kísértem el, s egy haldoklás búcsúkezével váltunk el (csaknem némán) azon egy zászló alól kétfelé küldetve, azzal a különbséggel, hogy ő a dicsőség templomába hatott fel, én pedig elestem.”22
A 60 év fölötti Bolyai borús visszatekintése alaptalan. Az utókornak egyre inkább sikerül bebizonyítania, hogy hazaérkezésével kitárult az erdélyi ifjúság számára egy fél évszázadig tartó korszerű tudományos oktatás lehetősége. A kör nem bezárult számára, inkább spirálként folytatódott. Bolyai marosvásárhelyi matematika-, fizika- és kémiaprofesszorként szinte lemásolta a göttingai oktatási módszereket. Közösen kísérletezett, vizsgálódott az általa oktatott szinte mindegyik természettudományos területen. Így egész nemzedékek sajátíthatták el a tudományos gazdálkodás, kemencerakás, borkezelés, egészséges életmód és ki tudja még hányféle területen a haladás, fejlődésre törekvés eszméit. Leglényegesebb oktatói érdeme az volt, hogy tudatosította az ok-okozati összefüggések kutatását, valamint a függvényszemlélet jelentőségét. Bolyai Farkast tekintik kora egyik leghaladóbb szellemiségű tanárának Erdélyben. Tanítványai közül számos világhírű tudós került ki. Első helyen említjük természetesen a fiát, aki megalapozta az abszolút geometriát. Az ő házitanítója Vajda Dániel borászati szakíró, akinek borai New Yorkban is eljutottak. De említhetjük (albisi) Bod Pétert, akinek jószágigazgatóként gróf Bethlen Ferenc birtokát európai hírű tette. Vályi Elek, Ercsei János, Horváth Farkas és az 50 éves tanári pálya alatt ki tudja hány tudós–gazdálkodó vitte szerte a Kárpát-medencében a mérésen, tudományos eljárásokon alapuló szakmai műveleteket. Ezért írta fia róla, hogy:
„Atyám egyszemélyben volt pomológus, kertész, borgazda, bororvos, betegeket elektrizáló és általán doctornak is oly nagy, hogy az igazi doctorokat elhagyva számosan sikerrel hozzá folyamodtak[…] mint kemencemester is országszerte híres[…] szinte minden múzsával polygámiában élt, […] belőle szinte minden kitelt volna.”
De térjünk vissza az Elemekhez. Bolyai Farkas szinte egész életében folytatta a „parallelák” – azaz a párhuzamosok axiómájával kapcsolatos vizsgálatait – eredménytelenül. De bármennyire is volt fontos számára az euklideszi axióma ellentmondásainak feloldása, amikor észrevette fia érdeklődését a párhuzamosok kérdése iránt, kétségbeesetten próbálta lebeszélni. 1820-ban ezt írja Bécsben tanuló fiának:
„A parallelákat azon az úton ne próbáld: tudom én azt az utat is mind végig – megmértem azt a feneketlen éjszakát én, és az életemnek minden világossága, minden őrőme kialudt benne – az Istenért kérlek! hagyj békét a paralleláknak – úgy irtózz tőlle, mint akármicsoda feslett társalkodástól, éppen úgy megfoszthat minden idődtől egésségedtől s egész életed boldogságától. […] én feltettem volt magamba, hogy feláldozzam magamat az igazságért, s kész lettem volna martyr lenni, csak hogy a Geometriát megtisztítva ezen mocsokból adhassam az emberi nemnek; […] visszatértem, mikor általláttam, hogy ennek az éjszakának a főldről fenekét érni nem lehet, vigasztalás nélkül, sajnálva magamat s a szegény emberi nemet. Tanulj te az én példámon; én a parallélákat akarva megtudni, tudatlan maradtam, életem s időm virágját mind az vette el – sőt minden azutáni hibámnak tőve mind ott volt s a házi fellegzésekból esett reá. Ha a parallélákat feltaláltam volna, ha senki se tudta volna is meg, hogy én találtam, angyal lettem volna.”23
Amint azt már a fentiekben említettük, Bolyai Jánosra nem hatottak apja intelmei, tovább vizsgálódott, és megoldotta a kétezer éves feladatot.
Bolyai János digitalizált marosvásárhelyi hagyatékában24 található az 1554 (1–11. pag.) jelzetű magyar nyelvű irat, ami nem Bolyai János kézírása. A teljesen különálló, címmel ellátott irat tetején idegen írással ez áll: „Bolyai János első Euklides tanulmányai” amit piros ceruzával írt egy harmadik személy, valószínűleg az a könyvtáros, aki Bolyai kéziratait rendezte. Az írás ugyanis nem Bolyai János kézírása, hanem feltehetően az iraton olvasható Horváth Farkas jegyezhette le. A többi (1–1553) irat római számokkal jelzett mappákban, saját jelzetükkel kerültek bejegyzésre. Az 1554-es jelzetű irat tartalmát tekintve Euklidész Elemek című munkája első könyvének bővített, kiegészített változata. Az irat katalógusban szereplő címe megegyezik az első oldal tetején olvashatóval
Az írás szerzője és keltezése tehát ismeretlen, de van egy fontos névbejegyzés az első oldal hátoldalán két szó közé apró betűkkel beszúrva: „Horváth Farkas”. Ez még nem bizonyítja, hogy az ő munkája. Mi azonban a továbbiakban ezt feltételezzük, mint igen valószínű tényt. Ha tehát Horváth Farkas írta, akkor feltehetően iskolai jegyzet, amit Bolyai professzor óráján diktálásra írt, vagy egy másik munkáról másolt. Horváth Farkas (született 1829) egyike volt Bolyai kiváló tanítványainak. 1844-ben subscribált a Marosvásárhelyi Kollégiumban. Bolyai Farkastól tanulta a matematikát és fizikát, gyakorlati mértant. Magánszorgalomból magas építészetből, út-, vasút-, víz- és hídépítészetből is vizsgát is tett. 1870. szeptember 27-én Pest város szolgálatába lépett, ahol elnyerte az újonnan szervezett katasztralis mérnöki állást, ugyan azon évben a József-műegyetemen földmérői oklevelet nyert. 1875-ben az Építész egyletben Bolyai Farkas kemenceszerkezeteiről tartott előadást, amit nyomtatásban is kiadott.25
A Bolyai kézirathagyaték 1554 jelzetű irata, amennyiben Horváth Farkas nevéhez kapcsolódik, keltezését tekintve tehát a 1840–44 közé tehető.
| 1655 | Néhány magyarra fordított részletet az Elemek-ből. = Apáczai Csere János: Magyar Enciklopédia. |
| 1840 körül | „Bolyai János első Euklides tanulmányai.” Lelőhelye: Marosvásárhely, Teleki–Bolyai Könyvtár, Bolyai gyűjtemény, Bolyai János iratok, 1554. számú irat. Az Elemek első könyvének bővített, kiegészített változata, amely – akárcsak a Brassai féle fordítás – 13 feladat megoldását tartalmazza. Az írás szerzőjének a neve is fellelhető az iraton, az első oldal hátoldalán (1554/1v) két fejezet közé apró, jól olvasható betűkkel, bekeretezve, beszúrva: „Horváth Farkas”. |
| 1865 | Euklides elemei XV könyv. Brassai Sámuel fordítása. MTA, Pest. |
| 1905 | Euklides: Az Elemek első hat könyve. Baumgartner Alajos fordítása. Franklin-Társulat, Budapest. |
| 1983 | Euklidész: Elemek. Mayer Gyula fordítása. Gondolat, Budapest. |
A négy változatot összehasonlítva érdekes megállapítások tehetők. A következőkben idézzük ugyanazt a részletet – első könyv, 1. feladat [tétel].

Euclides első könyve.
[1.] Feladat: Megadott ab egynre aequilatorum Δ ot construálni:
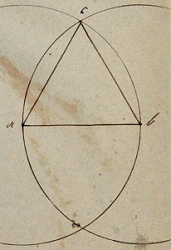
Megfejtés:27 Mind a, mind b pontokat középpontokkal véve, ab sugárral írt két kör ha egymást c ben vágja, ugyan c ről a ra is b be is egyenek vonatnak, abc lesz a kívánt Δ.
Okadat:28 Azt kelletvén meg mutatni, hogy a három oldal mindenik kettő egyenlő s világos lévén, hogy három közül csak három különböző pár vétethetik: ab és ac egyenlők, mert ugyanazon kör sugárai, ab is = ac (ugyanazon okból), ac pedig = cb mert mind a kettő ab hez egyenlő.
Jegyzet 1. Hogy a két kör vágja egymást könnyű megmutatni.
2. Azt is láthatni, hogy ha három dolog van u.m: a, b, c, minden külömböző párak kijőnek, ha a a’ b vel, s az után a’ c vel köttetik öszve, valamint a’ b is a’ c vel. De az aritmetikában megmutattatik, hogy akármely dologból vehető ambók29 száma = n·n–1
3. Megjegyzendő, hogy Euclides minden feladata megfejtésében constructio geometricat használ, azaz egyenhúzót30 és circalmat31 adván az ember kezébe. Csak kört szabad írni és egyent húzni, amazt megadott pontból, megadott sugárral, ezt megadott ponttól megadott pontig húzni és kinyújtani szabad.32
[2.] Feladat: Meg van adva a pont ’s bc egyen ’s ’a cb egyenhez egyenlő és a ban végződő egyent kell csinálni.
Megfejtés: a ról bc nek akármely végére vonattassék egyen ’s építtessék ac re Δ aequi:33, azután irassék c körül cb sugárral kör, mindaddig míg vágja dc oldal kinyújtását, a Δ tetejét d nek nevezve; legyen ezen sugár e ben és irassék kör de sugárral, ekkor da oldal kinyújtását f be vágja, af lesz a kívánt egyen.
Okadat: Mert cb=ce (ugyanazon kör sugarai) de=df (ugyanazon okból), dc=da (aequilaterum Δ oldalai) ce=af (egyenlőkből egyenlőket véve, egyenlők maradnak), bc is = ce tehát af=cb (ha két dolog egy 3-ikhoz egyenlő, egymást közt is egyenlő.)
Horváth Farkas [beszúrva, bekeretezve]
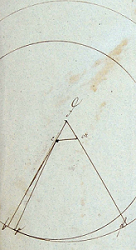
[3.] Feladat: Meg van adva két egyen ab és cd meg kell mondani egynelők-e vagy nem, s ha nem, a nagyobb mennyivel nagyobb a másiknál?
Sőt ki kell mutatni, mi lesz ha egyik a másikból subtráháltatik,34 ’s mekkora egyen lesz, ha egyik a másikhoz addáltatik?35
Megfejtés: Az előbbi szerént a-ból kezdődő, s a cd hez egyenlő egyent kell tenni, végződjék ez e ben, a körül ae sugárral kört kell írni, s ha ez az ab egyent éppen b ben vágja, akkor a cd egyen egyenlő az ab egyenhez. Hogy ha pedig az a és b közt f be vágja, akkor ae tehát cd is < ab nál fb vel. Ha pedig ae sugárral írt kör az ab kinyújtott részét g ben vágja, akkor cd ab nél bg vel >
Ha pedig cb egyent addálni kell ab hez, akkor cd hez egyenlő egyent kell tenni b ből legyen a bh, az ahol ez vágja az ab nek b féléi kinyújtását legyen i és ekkor ai lesz a keresett summa.
*1: Állítmány Ha két triangulumban36 két oldal a közbellő szöggel egyenlő, a harmadik oldal is egyenlő lesz, és a 2 valamint az egymásnak megfelelő szögök is.
Okadat: stb

Első Feladat:
Adott határzott egyenre egyenlőoldalu háromszeget állítani össze.

Legyen az adott határzott egyen AB.
Ezen AB határzott egyenre kell egyenlő oldalu háromszeget állítani össze.
A középponttal AB közzel írassék BCD kör, és megint B középponttal BA közzel írassék ACD kör, és a C ponttól, hol a körök egymást vágják, az A, B pontokhoz vonassanak CA, CB egyenek.
Minthogy az A pont, BCD körnek középpontja, AC egyenlő AB-vel; ismét mivel B pont ACD körnek középpontja, BC egyenlő BA-val. Meg vala mutatva, hogy CA egyenlő AB-vel, tehát mind CA mind CB egyenlők AB-vel. Ugy de azonegygyel egyenlők egymással is egyenlők, tehát CA egyenlő CB-vel; CA, AB, BC tehát mind hárman egyenlők egymással.
ABC háromszeg tehát egyenlőoldalu, és az adott határzott AB egyenre van összeállítva.
Tehát adott határzott egyenre egyenlőoldalu háromszeg állíttatott össze, mit mívelni kelle.
1. Adott határolt egyenesre szerkesszünk egyenlő oldalú háromszöget.
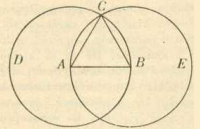
Legyen az adott határolt egyenes AB. Tehát az AB egyenesre szerkesszünk egyenlőoldalú háromszöget.
Rajzoljuk az A középpont köré az AB sugárral a BCD kört, viszont a B középpont körül a BA sugárral az ACE kört, és a C pontból, melyben a körök egymást metszik, húzzuk meg az A és B pontokhoz a CA és CB egyeneseket.
És minthogy az A pont a CDB kör középpontja, AC egyenlő AB-vel. Viszont, minthogy B pont a CAE kör középpontja, BC egyenlő BA-val. De azt is bebizonyítottuk, hogy CA egyenlő AB-vel. Ennélfogva mind CA, mind CB egyenlő AB-vel. Amik pedig ugyanazzal egyenlők, egymással is egyenlők (I. axióma). Ennélfogva CA egyenlő CB-vel. Tehát mind a három: a CA, az AB és a BC egymással egyenlő.
Az ABC háromszög tehát egyenlőoldalú. És megszerkesztettük az adott határolt AB egyenesre.
Adott határolt egyenesre tehát egyenlőoldalú háromszöget szerkesztettünk. Ezt kellett elvégeznünk.
I. 1. Tétel
Állítsunk adott véges egyenes szakasz fölé egyenlő oldalú háromszöget!
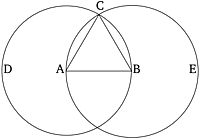
Legyen AB az adott véges egyenes szakasz. Az AB véges egyenes szakasz fölé kell tehát egyenlő oldalú háromszöget állítani.
Legyen BCD az A középpontú, AB távolsággal rajzolt kör (3. P.), továbbá ACE a B középpontú, BA távolsággal rajzolt kör, és a C pontból, amelyben metszik egymást a körök, illesszük az A, B pontokra a CA, CB egyeneseket (1. P.).
Minthogy az A pont középpontja a CDB körnek, AC egyenlő AB-vel, továbbá, minthogy a B pont középpontja a CAE körnek, BC egyenlő BA-val. De megmutattuk, hogy CA is egyenlő AB-vel, tehát CA és CB mindketten egyenlők AB-vel. Amik viszont ugyanazzal egyenlők, egymással is egyenlők, tehát CA is egyenlő CB-vel (1. Ax.), így CA, AB és BC mindhárman egyenlők egymással.
Tehát az ABC háromszög egyenlő oldalú, és az adott AB véges egyenes szakasz fölé állítottuk. Éppen ezt kellett megtenni.
A különféle magyar fordítások szövegével összevetve azt látjuk, hogy:
1. Feladat
2. Megfejtés
3. Okadat
4. Megjegyzés(ek)
Szakemberek számára több kutatási lehetőség is rejlik ebben az iratban, ami újabb adalékokkal szolgálhat mind a magyar, mind az egyetemes matematikatörténet számára: szakmai, szaknyelvészeti, pedagógiai, iskola-, könyvkiadás-, intézménytörténeti újdonságokat mindenképpen tartogat számunkra.
Igazán nagy eredmény az lenne, ha valamelyik tudományegyetemen akár szakdolgozati, akár doktori disszertáció témája lehetne ennek a kéziratnak teljes kritikai feldolgozása.
Az 1554-es irat fordítója – oktatási szempontokat figyelembe véve – az érthetőség céljából, a feladatmegoldáson belül az egybefolyó szöveget feldarabolta, alcímekre osztotta (megfejtés, okadat stb.) Szükség szerint számozással és aláhúzással is kiemelte a szöveg helyét, jelentőségét. Ma azt mondanánk, hogy a fordítói szabadság eszközeivel élve érthetőbben adta elő a feladat megoldásának lépéseit, mint akár az eredeti szöveg, akár a későbbi szöveghű fordítások.
Feltételezésünk az, hogy a fordítás Bolyai Farkastól származik, hiszen az Űrtan szövege 1850-ben már nyomdában volt. A latin nyelvű oktatásról a magyar nyelvre történő áttérést minden bizonnyal Bolyai Euklidész szövegével kezdte. Szokása szerint a jól rajzoló diákjai tisztázva lemásoltak egy-egy „leckét”, amit a később Bolyai összegyűjtött és továbbadta a következő évfolyamoknak. Sokszor egy évtizedig is közkézen forogtak az igényes jegyzetek szinte minden tantárgyból. Ma a több ezer oldalas diákjegyzet-gyűjtemény a Bolyaiak kézirathagyatékának részét képezi. Neves diákjegyzet szerzők: albisi Bod Péter, Ercsei János, Kendeffy Károly, Horváth Farkas.
A legfőbb kérdés az, hogy a címzés: „Bolyai János első Euklides tanulmányai” mit takar? A kézírás nem Bolyai Jánosé. Ha Horváth Farkas írta 1840 körül, akkor János már felnőtt férfi volt. Elképzelhető, hogy amikor János magyarra akarta fordítani az Appendixet kért apjától egy magyar nyelvű diákjegyzetet, hiszen saját állítása szerint küszködött a magyar nyelvű szakkifejezések hiányával. Így kerülhetett az 1554-es irat az ő kéziratai közé.
A digitalizált kézirat hozzáférhető a Teleki Téka honlapján.