
Az alábbi abránkon vázlat látható a Chartres-i katedrális északi oldalhajójának rózsaablakáról. A magyarázó ábra alsó fele kiemeli a kompozíció geometriai hátterét, másrészt mellőzi az itt vissza sem adható részleteket, színeket, szépségeket. A székesegyház a XIII. században épült, a francia gótika hírességeinek sorában, felhasználva a párizsi Notre Dame építészeti tanulságait, másfelől kevéssel a Reims-i és az Amiens-i katedrálisok előtt; mindegyiken látható több hasonló ún. mérmű(1). Ennek az ablaknak kb. 10 méter az átmérője, szerkezete hasonló a főhomlokzat rózsájához.
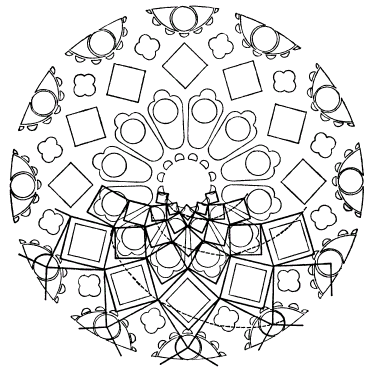
A legbelső, kis félkörökből álló ablakkoszorúhoz 12 kis négyzet kapcsolható, 1-1 közös csúcspárral – a szimmetriát nem is említjük –, közéjük újabb 12, és így tovább. A hatodik koszorú négyzeteinek csatlakozási csúcsai éppen a kereten levő kisebb körök középpontjaiba kerülnek.
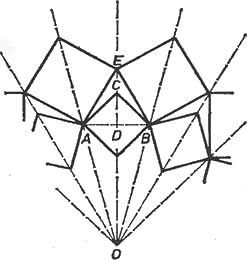
A második négyzet $OA$ tengelye 15°-kal van elfordulva $OC$-hez képest, ezért $OAE \sphericalangle =$ 15° és $BAE \sphericalangle =$ 60°, tehát $ABE$ szabályos háromszög, $AE = 2 \cdot AD = \sqrt{2} \cdot AC$, a négyzetek oldalai mértani sorozatot alkotnak.
A szaggatva berajzolt görbére felfűzött csúcsok mentén 45°-os elforduláshoz a vezérsugár $\sqrt{2}$-szörös növekedése tartozik. Az ilyen típusú görbéket logaritmikus spirálisnak nevezik.