Köszönet a segítségért Szilassi Lajosnak.
Klein-palackok síklapokból
Ismerőseim udvarias kérdésére, hogy mivel is foglalkozom mostanában, azt szoktam mondani, hogy Klein-palackok síkokra bontásával. A választ szinte azonnal követi a második kérdés: Az meg mi a szösz? S kezdhetem a magyarázkodást az alapoktól. Most abban a szerencsés helyzetben vagyok, hogy ezt Önök, nálam sokkal jobban tudják. Hogy mégis figyelemre méltatnak, hálásan köszönöm.

Rögtön pontosítanom kell a címet. Eredetileg az lett kiírva, hogy Klein-palackok síklapokból. Valójában, amit bemutatok, az nem a Klein-palack a maga valóságában, sokkal inkább annak ábrázolása. Ezt nem mentegetőzésnek szánom, csak tudni kell, hogy amit a kezükben tartanak, az egy kép. Még akkor is, ha térbeli. Nem tévesztendő össze az ideával, amiről szól. Ahogy a portrét sem tévesszük össze a modelljével. Az ábrázolásnak is megvannak a maga törvényei, ahogy az ideának, a matematikai objektumnak is. A helyes cím tehát így hangozna: Klein-palack ábrázolások síklapokból. Csakhogy, egyáltalán nem biztos, hogy a létrehozott tárgyaim valóban Klein-palackok. Ez vizsgálatra szorul. És ha némelyik nem bizonyul annak, akkor ne készítsem el? Egyiket elküldtem Szilassi Lajosnak, hogy nézze meg. Azt válaszolta, hogy az nem Klein-palack, hanem egy hét lapból álló zárt, nem irányítható felület. De ez ne szegje kedvemet. Nem szegte. A cím viszont újabb módosításra szorul. Zárt, nem irányítható felületek ábrázolása síklapokból. Nem hiszem, hogy tömegek özönlenének ide e cím hallatán. S még nem említettem, hogy a síkok, melyekből e testeket felépítem, mekkora jóindulattal nevezhetők síkoknak. Gránitból képes vagyok síkot faragni, mészkőből képes vagyok elhitetni a nézővel hogy síkot lát, de fóliából csak jelölni tudom. De a kalandhoz, melynek átéléséről megpróbálok beszámolni, talán ez az apparátus is elegendő.


Kalandozásaimhoz az inspirációt, McBride Charles Ryan építésziroda Ausztráliában épült háza adta. A leírás szerint az épület falainak és belső tereinek az elrendezése a Klein-palack elve alapján készült. A Klein-palack, vagy Klein-kancsó olyan egyoldalú, felület, mely fokozatosan önmagába fordulva, a nélkül záródik, hogy közben a térből kiharapna egy szeletet. Az ausztráliai épület egzotikumát nem pusztán a topológiai elrendezése adja, hanem az, hogy a Klein-palack motívumot az üvegfelületek, a tető és a falak, hatalmas síkokra bontják. A síkok a legkülönbözőbb szögekben találkoznak egymással, eltérve az építészet szokásos formavilágától. Az épület letisztult vonalai, a merész ötlet arra sarkalt, magam is megpróbálkozzak hasonló formák tervezésével.

by John Gollings and McBride Charles Ryan Architects
FORRÁS: worldarchitecturenews.com
Először azonban néhány sorban ismertetném, mi is ez a furcsa geometriai objektum, a Klein-palack.
Klein-palack, vagy Klein-kancsó: Nevét Felix Klein német matematikusról kapta. Egyoldalú (nem irányítható), zárt felület, melynek a külseje folyamatosan alakul át a belsejévé, vagyis ha a felületét elkezdenénk festeni, az ecset felemelése nélkül ki tudnánk mázolni az egészet, kívül-belül. Leggyakrabban lopótök alakú kancsóként ábrázolják, melynek elvékonyodó szára visszakanyarodva áthatol saját falán és belülről csatlakozik a felülethez. Ily módon nemcsak ábrázolható, hanem el is készíthető, teszem azt, üvegből.

FORRÁS: Google képkereső
Ám akár ábrázolni, akár kivitelezni kívánjuk, a Klein-palack 3 dimenziós tér korlátai között, nem hozható létre az említett önátmetszés nélkül. A Klein-palack matematikailag származtatható egy négyzetből, úgy, hogy a szemben lévő oldal párjai közül az egyiket azonos irányban a másikat fordított irányban ragasztjuk össze. A Klein-palack létrehozható két ellentétes csavarodású Möbius-szalag összeragasztásával. Ezt először David Hilbert írta le, s a műveletet később Szilassi Lajosnak sikerült egyetlen képlettel leírnia, s ezzel sima felületként ábrázolnia az említett Möbius-szalagot.
Fontos figyelmet szentelni, hogy a Klein-palack másik tulajdonságának, hogy felülete zárt. Azaz a Möbius-szalaggal ellentétben nincs éle. A Möbius-szalagnak egy éle van, mely duplán körbefutja a szalagot.

A Klein-palack nem rendelkezik élekkel. Olyan mintha addig csavargatnánk egy gumiszalagot, amíg nem irányítható felületté válik, és ezután hézagmentesen összedolgoznánk. A síklapokból épített Klein-kancsónak természetesen vannak élei, de ezek mindig két sík találkozásával jönnek létre, sohasem a felület széleként. Möbius szalag síkokra bontásakor is keletkezhetnek élek a síkok találkozásánál. Ezeket célszerű megkülönböztetni a szalagon körbefutó eredeti éltől. A dolog néha nem is olyan egyszerű. Példa erre Ulrich Brehm három síklapból szerkesztett Möbius-szalagja.
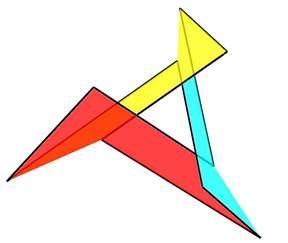

FORRÁS: Ulrich Brehm koordinátái alapján szerkesztette az Euler 3D programmal a Szerző. mathcurve.com
A Klein-palackot gyakran ábrázolják apró síklapokra bontva. Az esetek zömében a síklapokra bontás, a látvány értelmezését szolgálja, néha azonban megfigyelhető a síklapok számának csökkentésére irányuló törekvés. Ez a tendencia figyelhető meg, egy a Berkeley egyetem oldalán publikált mintegy 150 lapból álló Klein-palack szoborterven, valamint egy 24 lapból álló drezdai modellen.
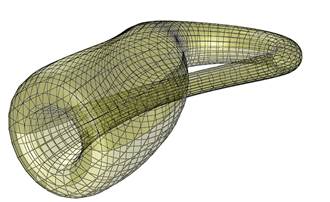
FORRÁS: Szilassi Lajos Euler 3D fájlja alapján
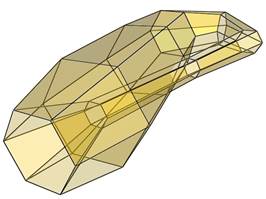
FORRÁS: Szilassi Lajos Euler 3D fájlja alapján

FORRÁS: math.tu-dresden.de

FORRÁS: Internet oldal. A szerző vélhetően Carlo H. Sequin
Ez a törekvés fertőzött meg engem is, amikor megpróbáltam minimalizálni a Klein-palackot alkotó síklapok számát. Tapasztalataim alapján a radikális oldalszámcsökkentés nem végezhető el mechanikusan. A sok intuíciót követelő tervezőmunka végén azonban a megszokott Klein-palackábrázolásoktól gyökeresen eltérő karrakterű látvánnyal szembesülünk.
Tekinthető-e poliédernek a síklapokból épített Klein-palack? Ehhez két feltétel teljesülése hiányzik: A Klein-palackon elkerülhetetlen az önátmetszés, síklapból építés esetén az önátmetsző síkok. A Klein-palack bár zárt felület, nem határolja körbe a tér egy részét, azaz nincs térfogata. Ennek ellenére nem árt, ha néhány poliéderekre is vonatkozó szabály érvényesül: A Klein-palack Euler karakterisztikája, a tóruszokhoz hasonlóan: 0.
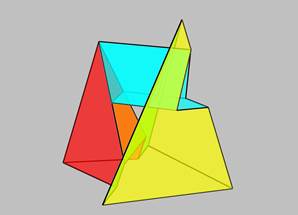

A síklapredukció néhány módja: Felfogható a Klein-palack dupla falú dobozként, ahol egy csatornával összekötöttük a külső, a belső majd a szemközti belső falat. Itt a járat véget ér, s két réteg közé jutunk. Érdemes a doboz, és a csatorna falait, a minél kevesebb síkból megszerkeszteni. Azaz, olyan poliédert találni, melynek legalább egy konkáv lappárja van. Öt síklapból már készíthető ilyen, s további lapokat kell a csatorna falának szánni. Ezzel a módszerrel készültek a C és a D sorozat Klein-palackjai.
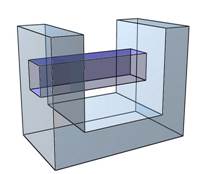
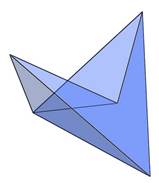

Egyes variációk csúcselrendezése megengedi szabályos testekbe való átszerkesztését. Nyolc síklap felhasználásával számos szabályos tetraéderbe szerkeszthető változat készíthető. Tizenegy lapból készült szabályos oktaéderbe írott változat. (D sorozat)


Ha a feladatot épülettervezésként fogjuk fel, kiindulhatunk az alaprajz, jellegzetes önmagába hurkolódó rajzolatából. Célszerű, a lehető legegyszerűbb alaprajzot készíteni, azaz, minél kevesebb egyenes szakaszból megszerkeszteni azt. Nem árt, ha sikerül megszabadulni a függőleges fal, vízszintes födém sztereotípiától, s próbáljuk meg a falakat gúlaszerűen néhány közös pontban találkoztatni. Így lapokat spórolunk, s a látvány is kezd gyökeresen eltérni a téma közismert ábrázolásaitól. Alaprajzra tükrözve a látványt síklapokból álló Klein-palackot kapunk.
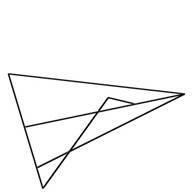
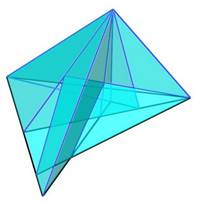
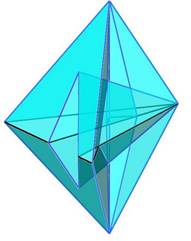
Egyes lapokat könnyedén közös síkba forgathatunk. Mikorra sikerül a lapok számát 11 körülire csökkenteni, kezd kialakulni a forma karraktere. Néhány a szimmetria síkra merőleges lap, és az őket körülvevő lappárok, melyek már nem forgathatók hasonló helyzetbe, anélkül, hogy összeomlana a rendszer. Ha, további síkoktól szeretnénk megszabadulni, más utat kell keresnünk. A 11 lapú Klein-palacknak még jócskán vannak háromszögletű oldalai. Ha ezeket sikerülne a tükörsíktól független, de páronként megfelelő helyzetű közös síkba rendezni, akkor, tovább csökkenthető az oldalak száma. A továbblépést jelentő intuíciót Szilassi-poliédernek köszönhetem. Szilassi Lajos szabályos tóruszait, különösen a kevés lapból állókat, jórészt „kellemetlenül hegyes szögű” konkáv hatszögek alkotják. Elképzelhető, hogy összefüggés lehet a kevés lap, és azok egzotikus alakja között. Próbáltam keresni a 11 lapú palackon olyan oldalakat, melyek nem elég furák. Így sikerült összevonni két pár háromszögletű lapot, konkáv ötszögekké. S a létrejött Klein-palack már csupán 9 lapból áll.
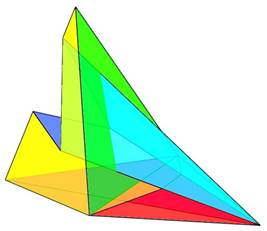
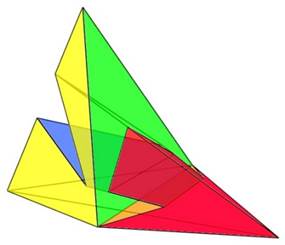
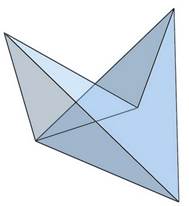
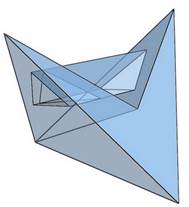
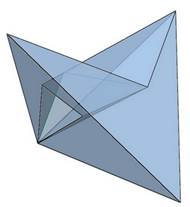
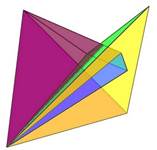
Az alsó síkokat két háromszög alkotja. Ezek, bár könnyen síkba hozhatóak, időbe tellett, míg beláttam nem a négy csúcsot kell egy síkba hoznom, hanem kettőt megtartva, további új csúcsokat kell keresnem. Másképp mondva, nem úgy kellett az alsó négyszöglaphoz jutnom, hogy elveszek a testből, hanem úgy hogy hozzáadok. Elképzeltem egy az említett két pontot tartalmazó síkot. A test síklapjait meg meghosszabbítottam addig, amíg az új alapsíkot el nem metszik. S az így létrejött forma már valóban 8 síklapból állt. Az ötszöglapok konkáv hatszögek, a hatszöglapok konkáv hétszögekké alakultak.
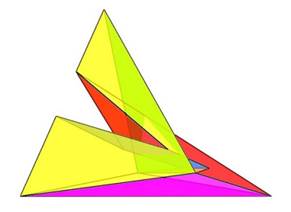

Szerkeszthető-e Klein-palack nyolcnál kevesebb síklapból? Létezik-e ilyen test? Lehet, hogy nem készíthető hét lapból Klein-palack, de azt esetleg tudhatjuk, hogy néz ki! A népszerű amerikai filmsorozat bűnügyi profilalkotóinak módszereivel képet alkothatunk arról, milyen is lehet a keresett objektum. Valószínűleg aszimmetrikus. A szimmetria ez esetben lappazarlást jelent. Nem a lapok száma, hanem azok elrendezése miatt. Bizonyára léteznek rajta kellemetlenül hegyes lapszögek és élszögek. Ez gyakorlatilag a lapok számának csökkenése miatt lép fel. Lesz rajta egy bejárat és egy alagút. Ez utóbbi feltételezés a gyakorlatban összeomlott. A bejáraton keresztül nem juthatunk messzire, az alagút pedig nullára zárul. Egyik hétlap jelöltbe sem lehet folyadékot tölteni. Az a korábbi feltétel sem teljesül, hogy ne legyen térfogata. Ami teljesül, a nem irányíthatóság és, hogy zárt felület, azaz nincsenek olyan élei, melyek a felület szélét határolják.
Készíthető-e Klein-palack, hétnél kevesebb síklapból? Nos, a Klein-palack felületén a térképszínezési feladathoz hat szín elegendő. Elképzelhető hogy készíthető Klein-palack felület hat tartományra osztva, és talán ezek a területek síklapokból is realizálhatóak, de ez egyáltalán nem biztos.
Alkothatunk-e profilt hat lapból épített Klein-palackra? Alig van elképzelésem, alakjáról, szerkezetéről. Gyaníthatóan többszörösen önátmetsző síkok gubanca lesz. Hegyes szögekkel, aszimmetrikus felépítéssel.

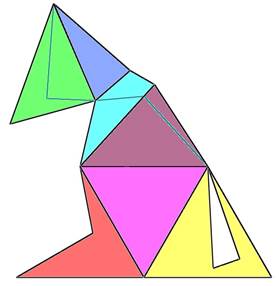
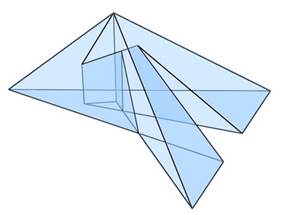
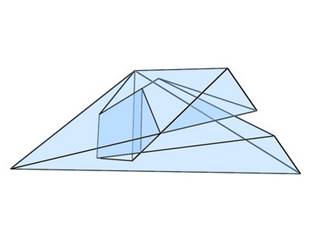
Óhatatlanul eljön az idő, amikor már nem elég csupán látnunk a vizsgált objektumot. A szellemi birtokbavétel megköveteli a test fizikai birtoklását. Akárhogy is, elő kell állítani azt az átkozott testet. A modellkészítéshez szükség van egy szabásmintára, mely alapján szerkesztett lapokból összeállítható a modell. Az Euler 3D program kiírja ugyan a csúcsok koordinátáit, ám ezek térbeli koordináták. A lapok megszerkesztéséhez viszont síkbeli koordinátákra van szükség. Kézenfekvő megoldás addig forgatni a testet, amíg a vizsgált lapja ráilleszkedik a koordinátarendszer valamelyik alapsíkjára. Az elforgatás szögének kiszámításához számológépet használtam, erre a program nem képes. Amint az adott lap ráilleszkedik az alapsíkra, az egyik érték nullára vált, a másik kettő érték pedig milliméterpapírra könnyen felszerkeszthető, ahonnan kartonpapírra másolható.
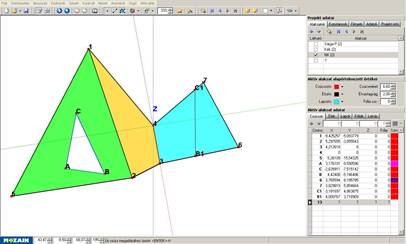
Fontos előre tisztázni a kartonpapírra jelölt lapok hajtogatási irányát. Ha a lapok konvex szögben találkoznak, akkor a karton színét, ha konkáv szögben találkoznak, akkor a karton fonákját kell megkarcolni. A ragasztást célszerű a belső, apróbb, bonyolultabb formákkal kezdeni, majd kifelé építkezve növeszteni a formát, s végül egy külső záró elem felhelyezésével befejezni. A tárgy, mely eddig elvi szinten létezett, most már kézzelfogható. Ellenőrizhető, hogy valóban bejárható-e a teljes felszíne, hogy valóban egyoldalú felületet tartunk-e a kezünkben. Az, hogy megfogható és forgatható nagyban segíti a megértés folyamatát, ám akad egy probléma: A kartonpapír nem átlátszó. A felületeket egy darabig követhetjük forma belső részei felé, de egy idő után csak logikánkra és képzeletünkre hagyatkozhatunk.



A modellépítés során végi fennállt az igény, átlátszó vagy áttetsző, s ez által áttekinthető makettek megépítésére. Különféle anyagokkal és technikákkal kísérleteztem, a nejlonzacskótól, a fém szúnyoghálón át, a feszítet sátorvászonig. Megvizsgáltam hogyan készíthető el plexiből, vagy üvegtáblákból. Problémaként jelent meg a különféle szögekben találkozó lapok egymáshoz rögzítése. Éles szögű találkozásnál a ragasztási felület jól láthatóan és kellemetlenül megnő, megszűnik a lapok egységes látványa.


Úgy döntöttem, első lépésben, papírvékonyságú, merev, átlátszó fóliával próbálkozom. Így talán kimodellezhető a technológiája egy nagyobb és erősebb változatnak is. Sajnos a keményfólia nem hajlítható a kartonpapírhoz hasonlóan, mert a karctű nyoma mentén törik. Ragasztása sem egyszerű, a Technokol Rapid és a pillanatragasztók csődöt mondanak, a ragasztópisztoly használata körülményes, s a fólián át minden hiba meglátszik. Ahogy láthatóak maradnak a kartonpapír modellek esetén ügyesen elrejthető ragasztási fülek is. Adódik a kézenfekvő lehetőség: az élhálózat vázként való felhasználása, ez azonban reménytelenül bonyolult feladat. Megfelelő szögekben és megfelelő profilúra csiszolt különböző teherbírású élek, nem képezhetnek erős, szilárd és esztétikusan egyszerű vázat. Valahogy csalni kell! Ha a test átlátszatlan lapokból megépíthető, akkor ilyen lapokból kell megépíteni. Ezzel megoldódik a ragasztás, későbbiekben hegesztés problémája, a csatlakozások erősek és elrejthetők.

Ugyanakkor semmi sem tiltja meg, hogy ezeket a nem átlátszó lapokat perforáljuk, és az eltávolított felületet átlátszó felülettel pótoljuk. Ha a lyuk megfelelően nagy, az eredeti lapnak csupán a külső széleit meghagyva, könnyen összeszerelhető erős és esztétikus vázat kapunk. A továbbiak csupán egyszerű technológiai problémák, akár egy tükör beillesztése a keretbe. S bár említettem, a fólia a fóliához nehezen ragasztható, a fólia a kartonpapírhoz már megfelelően ragad. Ezzel elhárult az utolsó akadály is az átlátszó színes modellek készítése elől.



Galéria























Pécsett, 2012. október 12-én

Festő: ?
Klein „Erlangeni programja”
Az Erlangeni program a geometria különféle alágainak újszerű, struktúraelméleti nézőpontból történő absztrakciója és összefoglalása volt, amit Klein 1872-ben fejtett ki, egyetemi székfoglaló előadásában, Erlangenben. (Az előadás később nyomtatásban is megjelent, több nyelven, A legújabb geometriai vizsgálatok összehasonlító áttekintése címen, de a matematikusok Erlangeni program néven idézik). A program nemcsak új, tömör szemléleti és módszertani keretet adott a geometria szerteágazó ágainak, hanem – ami ezzel együtt jár – az absztrakció „még be nem járt” tartományainak felderítésével, új elméletek születésére is lehetőséget adott. Minden olyan alapalakzatra építhető új geometria, amelyekre valamely transzformációcsoport alkalmazható. Klein Erlangeni programja az első olyan jelentős geometriai alkotás, amelyre nem mondhatjuk, hogy akár csíráiban is már az ógörögöknél létezett. Hatásai a geometriában mind a mai napig nyomon követhetők.