A görög matematika Euklidészt megelőző történelméről aligha van több forrásunk, mint néhány töredék Eudémosz-nak, Arisztotelész tanítványának A matematika története című művéből, melyeket Proklosz és mások hagytak ránk, továbbá különféle, Platón és Arisztotelész munkáiban elszórt megjegyzések. Ezért szívesen fogadunk bármilyen további, más területen lelt mégoly csekély információt.
Ebben a cikkben a görög városok érméin megjelenő matematikai vonatkozások közül mutatok be néhányat. E források természetüknél fogva kizárólag képiek, ám kétségkívül meggyőzőek.
Köszönetet mondok kollégámnak, Andreas Mehl-nek (Műszaki Főiskola, Ókortörténeti Tanszék, Darmstadt), akivel hasznos megbeszéléseket folytattunk filológiai és történelmi kérdésekről, és Maria R.-Alföldi professzorasszonynak numizmatikai tanácsaiért és egyedülálló gyűjteményéből átengedett képeiért.
Általános megjegyzések
Az archaikus és a klasszikus időkből származó görög érmék előlapja általában a kibocsátó város feliratát és jelképét viseli. A minket érdeklő képeket kivétel nélkül a hátlapon szemlélhetjük. Az ókori érmékről egyéb, általános ismereteket (technika, érték stb.) R.-Alföldi, Kraay vagy Seltman alapvető könyveiből nyerhetünk (lásd irodalomjegyzék). Az érméket a vonatkozó publikációban megjelenő számukkal azonosítjuk, mint pl. ’Kraay [szám]…’. Az érmékre vonatkozó évszámok egyértelműen Krisztus előtti időket jelölnek.
Mélosz
Mélosz – az Égei-tenger egyik szigete és városa – érméi nyilvánvaló matematikai
hatásról árulkodnak. A méloszi érmék előlapja almát (görögül:
μηλον) ábrázol, ami nem más, mint szójáték a sziget
nevével, míg hátlapján olykor a
 (méloszi) felirat jelenik meg. Két korábbi érme Kraay 124
Kr. e. 480 és Kraay 128 Kr. e. 450 körül hátlapjára átlósan osztott négyzet
vagy hasonlóan osztott kört vertek.
(méloszi) felirat jelenik meg. Két korábbi érme Kraay 124
Kr. e. 480 és Kraay 128 Kr. e. 450 körül hátlapjára átlósan osztott négyzet
vagy hasonlóan osztott kört vertek.



Kraay 124 (balra) és Kraay 128 (előlap és hátlap)
A sziget egyetlen, több mint nyolcvan érméből álló leletét – melyre 1907-ben bukkantak rá –, Kraay [1964] alaposan elemezte, s arra a következtetésre jutott, hogy az érmék mindegyikét 426–416 körül verték. (Méloszt az athéniak Kr. e. 416-ban lerombolták.) Az egyértelmű számozás céljából az M betűt használom a Kraay-cikkben megjelenő számok jelzésére, míg a betűjelzést nélkülöző számok Kraay könyvére [1976] utalnak.
Az M21, M33, M34 érméken nyolc háromszögre osztott négyzet látható:

Kraay M33
Ez ugyanaz a geometriai ábra, melyet Menonjában 82b–85b Platón ír körül, amikor a négyzet kétszeresét magyarázza. Az elemi geometriának ez az eleme olyan közismert lehetett, hogy utat talált az érmék díszítéséhez is.
Az ábra maga ősrégi, már olyan, régi babiloni ékírásos táblákon is látható, mint például a BM [British Museum] 15285 (előlap, vö.: Neugebauer 1. kötet, 137. p. és 2. kötet 3. tábla). A képet Hoyrup-tól 1987, 68a p. kölcsönöztük. A négyzet szerkesztését négy egyenlőszárú háromszögből Platón másodszor tárgyalja Timaioszában 55b, amikor a kockát mint szabályos poliédert írja le.
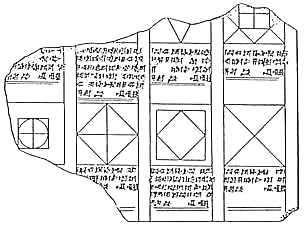
Régi babiloni matematikai szöveg
Az M3-on pontosan ábrázolt ötágú csillag (pentagram) is kétségtelenül matematikai eredetre vall.

Kraay M3
A szabályos ötszög átlói kulcsszerepet játszanak az ötszög szerkesztésében, amely Euklidész egyik jelentős tétele (XIII, 8). Korábbi, negyedik könyvében Euklidész ezt még bármiféle motivációt nélkülöző eljárásában elleplezi. Az ötágú csillag továbbá – úgy tűnik fel – a pitagoreusok szimbóluma volt, ahogyan azt Lucan, a Kr. u. 2. században élt szerző De lapsu in salutando 5, és Scholium to Aristophanes’ Nubes, 609. p.; lásd bővebben: van der Waerden [1979], 179. p. állítja. Tudomásom szerint ez az egyetlen, pontosan ábrázolt ötágú csillag a klasszikus görög periódusból (Kr. e. 500–300 körül). Erre a szimbólumra még visszatérünk, amikor majd Metapontum érméiről esik szó.
A méloszi érmemetszők matematikai hajlama más módon is megnyilvánul. A lelet két-, három-, négy-, öt-, hat-, hét-, nyolcszoros szimmetriát mutató érméket is tartalmaz. A Kraay által készített jegyzék 46 különféle típusú érmét sorol fel, közülük harmincegynek a hátlapján szimmetrikus a rajzolat.
Kétszeres szimmetria
A holdsarló (vagy félhold) Kraay M7–M12 többféleképpen is megjelenik. A kettős (bilaterális) szimmetria több motívum természetes jellemzője, és néhány más érmén is fellelhető M6, M23, M41, M44, M45. Nem állítható, hogy tervezőjüknek bármiféle matematikai törekvése lett volna:

Kraay M8
Háromszoros szimmetria
(a) Három delfin úszkál a középpont körül Kraay M4, M42, M43:

Kraay M42
(b) „Triszkelész” (háromszárú idom), három emberi láb Kraay M29, M35, M36:

Kraay M36
Négyszeres szimmetria
(a) Négyküllős kerék Kraay M13, M14, M15, M16. A görög érméken szokásos motívum, lásd Khalkisz és Phliusz alatt:

Kraay M15
(b) Négy árpaszem csillagalakban Kraay M19 (9. ábra). Ez az elrendezés egy hasonló, Metapontumból származó, öt szemet ábrázoló érmére emlékeztet, melyet az alábbiakban tárgyalunk.

Kraay M19
(c) Díszes négyágú csillag Kraay M20:

Kraay M20
(d) Széles szalagokkal négy részre osztott kör alakú bemélyedés, egyszerű kereszt Kraay M22. Ez az érme hasonló az alább tárgyalt hat részes, szimmetrikus, M39 jelű érméhez. Az egyszerű mintából az érmemetsző matematikai törekvése különösen kiviláglik:

Kraay M22
(e) A ’Menón minta’: négyzet, melyet négy kiemelkedő és négy bemélyedő háromszög alkot Kraay M21, M33, M34 (2. ábra).
Ötszörös szimmetria
Erre a legjobb példa az M3 jelű, ötágú csillagot ábrázoló érme Kraay M3.

Hatszoros szimmetria
Hasonló az M22-höz. A kört három átmérője hat egybevágó részre osztja Kraay M39, M40:

Kraay M39
Hétszeres szimmetria
Hét szirmú virág Kraay M17:

Kraay M17
Nyolcszoros szimmetria
(a) Nyolc szirmú virág Kraay M24 (ábra nélkül).
(b) Nyolc ágú csillag Kraay M46:

Kraay M46
Természetesen elgondolkodhatunk azon, miért éppen a Mélosz szigetiek érméi mutatnak ilyen, erősen matematikai jellegű rajzolatot. Egy lehetséges magyarázat: Kraay 1964, 16. és 19. p. szerint a méloszi lelet érméit rövid idő alatt sajtolták 416 előtt abból a célból, hogy pénzt teremtsenek az athéniaktól megtámadott Mélosz védelméhez. Halvány hasonlóságot láthatunk a méloszi érmék és néhány Metapontumból származó érme között. Ennek talán az az oka, hogy a mélosziak – szükséghelyzetben – ezüstjük mielőbbi érmévé verése céljából Metapontumtól béreltek érmemetszőt, aki matematikai érdeklődését követve készítette el a hátlap rajzolatát, amely legalábbis összhangban volt korábban vert pénzeivel.
Euklidész az Elemek negyedik könyvében szól a kör egyenlő részekre való felosztásának matematikai elméletéről, vagyis a szabályos sokszögek szerkesztéséről. Egy magyarázója szerint a IV. Könyv tételei eredete a pitagoreusokra nyúlik vissza. Részletesen lásd: Neuenschwander [1972]. Ez ismét Metapontum felé fordítja figyelmünket, ahol – feltehetően – Püthagorasz meghalt.
Metapontum
A görög szárazföldi és a szicíliai érmeknek jól meghatározott kronológiája van, mely annak köszönhető, hogy az érméket Athén és Szürakuszai jól ismert történetébe lehetett illeszteni. Ilyen időrendi skála Dél-Itáliában (Magna Graecia) nem áll rendelkezésünkre, így a numizmatikai kronológia bizonytalan és tétova Kraay [1974, 161. p.]. Seltman egyenesen Püthagorasznak tulajdonítja az érmeverés bevezetését Magna Graeciába, különösen a metszetmélynyomás (intaglio) technikáját, mikor is az előlap domborzata (relief) mint mélynyomat ismétlődik meg a hátlapon Seltman, 68. p.. Ez egyáltalán nem valószínűtlen, mivel Püthagorasz apja, mint azt Diogenes Laertius állítja De vita et moribus philosophorum VIII 1, kb. Kr. e. 250 gemmametsző volt, de egyéb érvek ezt, enyhén szólva, kevéssé igazolják vö. R.-Alföldi, I. kötet, 93. p.. Szamosz szigetét Püthagorasz Kr. e. 530 körül (az időpont felettébb bizonytalan) elhagyta és Magna Graeciába költözött, először Krotón városába, majd Metapontumba, ahol követői számára iskolát alapított. Püthagorasz életéről és iskolájáról lásd: Burkert [1962] és van der Waerden [1979]. Iskolájának hatása néhány későbbi érmén jelenhet meg.


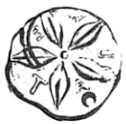
Kraay M 595 (előlap és hátlap) és BMC Italy 45
A pentagramot mint a pitagoreusok szimbólumát már említettük. A 15. ábrán két, feltűnően ötszörös szimmetriáról árulkodó érmét láthatunk Metapontumból. A baloldali érmét Kraay szerint Kr. e. 440 körül verhették. Előlapján a Metapontumra jellemző árpakalász a META felirattal, hátlapján árpaszemek négy ágú csillag alakzatban. Hasonló rajzolatot mutat a BMC (British Museum Collection) Itália, Metapontum 45 jelű érme hátlapja, mely rajzolat fölé egy máshol talált, korábbi érmén mintegy jelzésként kis félholdat nyomtak. Ez utóbbi érmét Kr. e. 440 körül verhették, nem sokkal korábban, mint a méloszi érméket (420 körül). Néhány méloszi érmén kitüntetett szerepet játszik a félhold. Kraay M19 jelű, méloszi érméje hátlapján – hasonlóan a metapontumi érmékhez – négy, csillagalakban elrendezett szem látható. Mint fentebb említettük, elképzelhető, hogy az érmemetsző Metapontumból ment Méloszra. Annak, hogy a szemek árpaszemek, e feltevés szempontjából érdektelen, az árpának vallási jelentősége van. Vö. Burkert [1977], 102. p.
A pitagoreusok valamikor 460 és 440 között politikai hatalmukat vesztették, ami megegyezik az érme verésének ugyancsak bizonytalan, 440 körüli időpontjával. (A pitagoreusok politikai történetét lásd ismét Burkert és van der Waerden írásaiban.)
Kis pentagramokat mint másodlagos szimbólumokat vagy jelzéseket sok későbbi érmén is találhatunk. Ennek tipikus példája Kraay 705 jelű érméje Veliából (Elia) (Magna Graecia), a 320 körüli évekből:

Kraay M 705 Veliából, 320 körül
A British Museum Collection katalógusa hat más, Itália különféle helyeiről származó érmét is tartalmaz, kettőt Sziciliából, kis pentagramokkal.
Akad ugyan néhány más lelőhely, de egészében véve az érmék zömét Magna Graeciában találták. Ez ugyanúgy tulajdonítható a pitagoreus hatás kései nyomainak, mint épp ellenkezőleg annak, hogy a pitagoreusok az etruszkoktól szerezték ismereteiket a pentagramról és a tizenkét lapú poliéderről. Szépen mintázott, etruszk eredetű szabályos tizenkét lapú poliédereket láthatunk Perugia archeológiai múzeumában számos egyéb, Nyugat-Európából, főleg a Nyugati Alpokból származó tizenkét lapú poliéderrel együtt a Krisztus születése utáni időkből. Részletes történeti leírását lásd Herz–Fischler [1987], különösen III. fejezet, 52–62. p.
Körülbelül Kr. u. 480-ig Éjina városa (és szigete) az Égei-tenger kereskedelmi központja volt. Éjina lakói voltak e régióban az elsők, akik érméket vertek. 480 után az athéniak versenytársukká váltak, s végül 430-ban szigetükről el is űzték őket. A peloponnészoszi háború végét követően, 404-ben visszatértek és ismét bocsátottak ki érméket, de korábbi jelentőségét a nép képtelen volt visszanyerni. Éjina érméi hátlapján mindig megjelenik a tengeri teknős vagy a teknősbéka, s mint egyébként, érdeklődésünket ezúttal is a hátlap mintájára fordítjuk:



Aeginából, Kr. e. 580–540 körül
Kr. e. 480-ig különféle mintázatú nyomatok jelennek meg, amelyek szimmetria-tengelyeikkel felosztott négyzetekből eredeztethetők. A 480–431 körüli időktől fogva aszimmetrikusan – mindig ugyanolyan módon – formázott mintákat találunk Kraay 123 és 127.
A Kr. u. 404-et követő idők új érméi Kraay 137 és 138 matematikai, derékszögű rajzolatot mutatnak. Ezek pontosan megfelelnek Euklidész Tételei II. 4. ábráival, csak a kisebb négyzet átlója hiányzik (18. és 19. ábra).


500–431 körül (balra) és 404 után (Franke–Hirmer, 335 és 336)

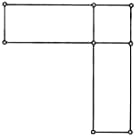
Euklidész (balra); Gnomón (jobbra)
Az Euklidész II. 4. a binomiális tétel – (a + b)2 = a2 + 2ab + b2 – geometriai változata. Hasonlóan felosztott téglalapokat és paralelogrammákat bőségesen találunk az Elemekben. Az ún. gnómón szokásos eszköze a matematikai (és a geometriai) bizonyításoknak. A kis négyzet hiányzó átlója talán éppen a gnómón hangsúlyozását szolgálja.
Tudjuk, hogy a khioszi Hippokratész volt az első, aki – Kr. e. 430 körül (Athénban?) – a matematika Elemeiről írt. Számomra világosnak látszik, hogy az Éjinából származó érmék hátlapjának megváltoztatása a matematika megújított tudománya hatásának köszönhető.
Khalkisz
Khalkisz Euboea szigetének egyik legjelentősebb városa. Kraay [1974, 89–90. p.] és Chantraine [1958] szerint Khalkisz matematikai szempontból érdekes érmét az 530–470 közötti időszakban verték, vagyis sokkal korábban, mint az eddig tanulmányozott érméket. Az előlapon sas vagy, a 480 körüli évek után a karmai közt kígyót tartó sas látható. A hátlapon
„négy-, öt- vagy háromküllős kerék és a ΥΔΛ betűk jelennek meg kissé benyomott háromszögben vagy négyzetben”.
A Khalkiszból származó első kerekek (515 körül) a hátlapon korábban megjelenő kvadriga (négylovas harci- vagy versenyszekér) egyszerűsített képei lehettek. Kraay 264 jelű érméje egyértelműen tényleges szekérkereket ábrázol, s nem annak matematikai absztrakcióját. A helyzet egészen más a 485 után vert érmék esetében. Mint a 21. ábrán látható, gyakran találunk háromszögbe vagy négyzetbe írt kört, melyet szabályos három-, négy- vagy ötszögre osztottak fel, pontosan úgy, ahogyan Euklidész negyedik könyvében.

Khalkisz, 480 körül (Franke–Hirmer)
A hátlap veretét mint egyenlő oldalú (Kraay 265) vagy derékszögű Seltman, IV. tábla, 16 és 17 háromszöget aligha értelmezhetjük másképp, mint matematikai motívumként.
Kraay 265 jelű érméje geometriai ábrájához (egyenlő oldalú háromszög a beléírt körrel, melyet két, egymásra merőleges átmérő oszt fel) hasonló jelenik meg ismét egy középkori kéziratban, jelesül az ún. pszeudo-Boethiusi Geometria II-ben lásd Folkerts [1970], 224. p., 116. ábra:
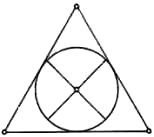
Boethius Elemek-fordításából
Ezt az ábrát a Geometria II-nek az a része tartalmazza, melyet Boethius fordított (görögből latinra, Kr. u. 505 körül, Folkerts, 72. p.). Ezt – még pontosabban – Euklidész IV. Könyve 3. feladata így fogalmazza meg: „Adott háromszöggel egyenlőszögű háromszög köré írható adott körről”. Euklidésznek magának „jobb” (vagyis a feladathoz és megoldásához jobb) az ábrája. A Geometria II néhány más ábrája pontosan megegyezik Euklidész Elemei II. Könyvének meglehetősen bonyolult ábráival (Folkerts, 223., 100. és 101. p.). Ha elfogadjuk, hogy a Geometria II ábrái – legalábbis azok, amelyek Boethius Euklidész-fordításához tartoznak – a késői ókorba nyúlnak vissza, úgy még egy példánk van Kraay 265 jelű khalkiszi érméjére:




Kraay 265 és 266 (balra); Seltman, IV. tábla, 16 és 17 (jobbra)
Mindazonáltal évezrednyi a különbség az érmék keletkezésének és Boethius működésének időszaka között. Lehetséges, hogy az ókori ábrákban megjelenő kört két, egymásra merőleges átmérővel rajzolták meg? Ez megfelelne a fentebb bemutatott ékírásos tábláknak, Euklidész IV, 6–9-nek és a görög érméken látható sok egyéb ’kerék’-nek.
A matematika történetének szemszögéből nézve a Kr. e. 530–570 közötti évek Püthagorasz és közvetlen követőinek időszaka, s ötszög iránti érdeklődésüket már említettük. Hippaszosz dodekaédere ugyancsak e témához tartozik, lásd: van der Waerden [1979], Pythagoreer 71–72. p., Iamblichus Vita Pythagoras 88, 246–247. p. Iamblikhosz, a Kr. e. 3. évszázadban élt filozófus halvány célzást tesz a késői pitagoreusok és Khalkisz – vagy legalábbis testvérvárosai – kapcsolatára, amikor így ír:
„A legjelentősebb pitagoreusok Phanton, Ekhekratész, Polümnésztosz és Dioklész Phliuszból és Xenophilosz a trák félszigetről, Khalkidike-ről.”
Iamblikhosz a késői pitagoreusokról beszél, biztosan a 480 utániakról. Mindazonáltal Khalkidike számos települése közül Khalkisz volt az anyaváros. Alább néhány, Abdérából származó érmét láthatunk (Kr. e. 430 körüli időkből), melyek újabb jelét adják annak, hogy a pitagoreusok ezen a vidéken is jelen voltak.
A peloponnészoszi várost, Phliuszt Iamblikhosz mint néhány késői pitagoreus működésének helyszínét említi. Kr. e. 420-ból származó érméi hátlapján, akárcsak a Khalkiszi érmekén, négyküllős kerék látható Kraay 302–304. p.. A Kraay által jegyzékbe vett érmék közül néhány a hátlapján ugyancsak kereket ábrázol, de mindegyikük egyedinek látszik (egy Athénből, 540 körül, kettő makedóniai törzsektől, egy a boiótiai Tanagrából).
A pitagoreusokkal való kapcsolatot ugyan kiemeltem, mindazonáltal világos, hogy a korai Görögországban nemcsak pitagoreusok voltak, hanem egyéb matematikusok is. Erről bővebben és alaposabban Burkert [1962] ír a pitagoreusi matematikusokról szóló fejezetében.
Abdéra
A trákiai Abdéra és jón anyavárosa, Teosz érmeinek előlapja ugyanazt a griffmadarat – mint a polgárság jelképét – ábrázolja. Abdéra vert pénzeinek jellemző vonása, hogy megjelenítik a pénzverő vagy a magiszter nevét. A 470-es éveket követően ezek a nevek teljességükben jelennek meg a hátlapok a mélyen metszett négyzet körül, amelyet viszont különféle istenségek, élettelen tárgyak, állatok vagy egyebek töltenek ki. Egyikükön, 430 körül
„Püthagorasz neve és egy szakállas fej látható, mely aligha akart volna mást, mint az előző évszázadban élt híres filozófust ábrázolni.”
A művészettörténészek szkeptikusan szemlélik történelmi személyiségek portréját a Kr. e. ötödik századból származó érméken. Mindazonáltal ismét Seltmant idézem, aki hangsúlyozza a jól ismert abdérai filozófiai iskolával (Prótagorasz, Démokritosz) fennálló kapcsolatot:
„Nem hagyhatjuk figyelmen kívül az ünnepelt filozófiai iskolával való kapcsolatot, melynek az abdérai Démokritosz, az atomista volt legfényesebb alakja. Születésének időpontját rendszerint Kr. e. 460 körülre teszik, neve megjelenik egy érmén…”
Az érmét Seltman jegyzéke nem tartalmazza, de létezik négy érme Démokritosz nevével a Kr. e. 415 körüli évekből, lásd: May, 234–237. p.
„Démokritosz is Püthagorasz nagy csodálója volt [Diogenes Laertius IX, 38 szerint] … és, minthogy a filozófia divat volt abdérában, egyikük [egy magiszter], aki a Püthagorasz nevet viselte, híres névrokonának idealizált portréját választotta hivatali évének jelképéül. Semmilyen más módon nem magyarázhatjuk, miért ábrázol ez a nevezetes érme egy finoman kidolgozott szakállas fejet, melyet a ΠΥΘΑΓΟΡΗΣ név vesz körül:”

Seltman, XXVIII. tábla, 11.
„Ez a négydrachmás, a szobrászat történetének kiemelkedő jelentőségű emléke a Kr. e. 432 előtti időkből, az első eredeti, megmaradt, névvel ellátott portré az időszámításunk előtti ötödik századból.”
Minthogy az érmét hetven évvel Püthagorasz halála után verték, a portré aligha akart a mai értelemben valóságos képmás lenni, ami a két különböző érméből is kitűnik. S hogy nem egy magiszter portréja, arra egyéb abdérai érmékből következtethetünk – lásd például Kraay 530–542 –, melyek esetében a név és a szimbólum egymással kapcsolatban áll, de nevezetes érménk kivételével portrét nem ábrázol.
Kör és ellipszis Szürakuszaiban
Vitruvius, a római építész De Architectura című művének hetedik könyve bevezetésében Anaxagorász és Démokritosz könyveit említi, melyekben színházi színpadok valamiféle perspektivikus tervezéséről szólnak. Részletesebben lásd: van der Waerden [1966], Erw. Wiss. 224–226. p.. A művészeti megjelenítés változása, vagyis elölnézete helyett a tárgy valamiféle perspektivikus ábrázolása először Szürakuszai érmein figyelhető meg.
„A Kr. e. 425 körüli időkig a Szürakuszai-i és minden egyéb érméken a kvadriga látható, ritka kivételként [lóval] nyugodtan lépkedve a győzelmi oszloptól. Ezt követően a lovakat – mintegy a versenyzés folyamatában – mindig ügetve ábrázolták.”
Ez utóbbi érméken a kvadriga a verseny legdrámaibb pillanatában jelenik meg: a lovak teljes sebességgel vágtatnak a forduló-oszlop körül, a szekér kerekei pedig ferde nézetben, ellipszisként vannak ábrázolva. A megjelenítés változását Kraay 807 (a kerék kör alakú) és Kraay 808 (a kerék ellipszis alakú) jelű érméin követhetjük nyomon:


Kerekek mint körök vagy ellipszisek (Franke–Hirmer)
Az érmék keletkezésének időpontja összhangban van Anaxagorász (500–428) és Démokritosz működésének idejével (460–380), így ebben az esetben a művészeti gyakorlat és az elméleti reflexió párhuzamos fejlődését tapasztalhatjuk.
A kutatók általában megegyeznek abba, hogy Menaekhmosz (Eratoszthenész szerint 350 körül, Platón akadémiáján) tanulmányozta először a kúpszeleteket részletesebben lásd: van der Waerden [1966], Erw. Wiss. 265–267. és 331–334. p., vagy mélyreható elemzését Knorr [1986], 3. és 4. fejezetében.
Ha ellipsziseket látunk Menaekhmosz előtt mintegy hetven évvel, úgy feltehetjük hogy a matematikusok már korábban is foglalkozhattak velük. Valójában már Démokritoszt is foglalkoztatta – atomelméletével összefüggésben – a kúpszeletek kérdése van der Waerden, 228. p.. Egyéb forrásunk azonban Euklidészt megelőző, azaz a Kr. e. 300 előtti időkből nincsen. Euklidész Optikájában a következő, 36. tételt olvashatjuk.
„A szekér kerekeit olykor körnek, olykor (ferdén) rajzolva látjuk.”
Ennek bizonyítására egy előbbi (segéd)tételt használ, s hozzáteszi, hogy a ferde nézetben az egyik átmérő maximális, a másik minimális hosszúságúnak látszik, míg a többi hossza e kettő között van. Egyetlen szó sem esik kúp- (vagy henger-)szeletekről! Másrészről nyilvánvaló a célzás az érméken látható művészi ábrázolásra: midőn a szekér hirtelen irányt változtat a forduló-oszlop körül, a kerekek ferde látványa tárul elénk.
Más, matematikailag megegyező esetben Euklidész együtt említi a kúpot és a hengert:
„Ha egy kúpot vagy egy hengert az alapjával nem párhuzamos síkkal metszünk, a metszet egy hegyesszögű kúp – pajzshoz hasonló – metszete lesz.”
A Jelenségek csillagászati értekezés sok ábrával, ahol a szférákat ábrázoló köröket rosszul, mint lencséket, s nem mint ellipsziseket ábrázolták vö. Euklidész–Heiberg, VIII. kötet. A ’pajzshoz hasonló’ jelentése: elliptikus; Euklidész korában a terminológia még kialakulatlan volt. A szekér kerekei azonban „az alappal párhuzamos” síkban fekszenek, kör alakúak, így a helyzet kissé más. A kerekek elliptikus alakjáról még Theón (380 körül) Euklidész Optikájáról írt recenziójában sem esik szó. Még furcsábbnak látszik, hogy a kerekek tényleges alakjának körülírására nem törekedtek, holott Euklidész maga négy könyvet írt a kúpokról. A modern matematikusokkal ellentétben, akik büszkék, ha felfedezik a különféle jelenségek összefüggéseit, jól elkülönítetten kezeli az optikát és a matematikát, s észrevehetően óvakodik átlépni a kettejük között létesített határokat.
Ezzel eljutottunk a megfigyeléseinket záró általános megjegyzésig. Fájdalom, nem tudunk túl sokat az ókori görögség általános kulturális körülményei között virágzó matematikáról. A görög érméket és általában a matematikát mai szemmel látjuk, és – mint Goethe mondja – az ember azt látja, amit tud.