Az isteni szülöttnek azonban van egy körforgása – ezután következik a híres platóni párosító szám, Az állam legrejtélyesebb, sokat vitatott részlete. A párosító számról szóló szöveg második része (onnan, hogy: „E számok négyharmados alapja…”) elég jól lefordítható, és nagyjából meg is van fejtve. Problematikus az első rész, és ebben is főleg a „homoiúntón” te kai anomoiúntón kai auxontón kai phtinontón” kettős genitivusza, amely bizony elég ügyetlenül lebeg a mondatban. Ha a jóval előtte álló „auxészeisz” függvényének tekintjük, ahogy ezt Schleiermacher, James Adam és Karl Vretska teszi, akkor a szövegben közölt verziót kapjuk. Ha viszont Arthur Ahlverst követjük, és a szót a rákövetkező „pantá”-hoz kapcsoljuk, akkor a következő változatot kapjuk:
„Az isteni szülöttnek azonban van egy körforgása, amelyet egy tökéletes szám foglal magába, az emberi szülöttét pedig egy olyan szám, amelyben először uralkodó és alávetett sokszorozások három távolságot és négy határt [nagyságrendet] véve fel, hasonlók és nem hasonlók, növekvők és fogyók valamennyi része közt racionálisan kifejezhető viszonyt teremtenek.”
„Az isteni szülöttnek azonban van egy körforgása, amelyet egy tökéletes szám foglal magába, az emberi szülöttét pedig egy olyan szám, amelyben mint elsőben [vagyis legkisebben] uralkodó és alávetett sokszorozások az egyenlővé tevőknek és a különbözővé tevőknek, a növekvőknek és a csökkentőknek három távolságát és négy határát alkotják, mindent megfelelővé és egymással összemérhetővé téve.”
Arthur Ahlvers verzióját már azért is érdemes figyelembe venni, mivel a párosítási szám és az egész szöveg megfejtésében ő jutott a legmesszebbre, és a most következő magyarázatokban az ő gondolatmenetét ismertetem.
Vegyük szemügyre először a szöveg könnyebben megfejthető elemeit:
„E számok négyharmados alapja öttel társítva és háromszor megszorozva két harmóniát alkot: az egyik úgy jön létre, ha az egyenlőt egyenlővel és a százat százzal megszorozzuk, a másik pedig egyrészt egyenlő [négyzetes], másrészt nem egyenlő [téglalap alakú] tényezőkből tevődik össze, vagyis az öt racionális átlóinak százszoros négyzete, mindegyikből levonva egyet, az irracionális átlóké, mindegyikből levonva kettőt, továbbá három köbének a százszorosa. Ez az egész egy mértani szám […]”.
a) „az öt racionális átlóinak százszoros négyzete, mindegyikből levonva egyet”
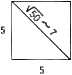
„az irracionális átlóké, mindegyikből levonva kettőt”
Az átmérő kiszámítása:
$$d^{2} = 2 \cdot 5^{2}; d^{2} = 50; d = \sqrt{50} = 7…$$ $$100 \cdot (\sqrt{50^{2}}–2) = 100 \cdot 48 = 4800$$b) „három köbének a százszorosa”:
$$100 \cdot 3^{3} = 100 \cdot 27 = 2700$$(Proklosz ezt a két számot összeadta, de ez nem bizonyult termékeny ötletnek.)
Hultsch fedezte fel (1882-ben-megjelent, dolgozatában: Die geometrische Zahl), hogy a fenti két számot nem összeadni kell, hanem összeszorozni:
$$4800 \cdot 2700 = 12\ 960\ 000$$Ez tehát az úgynevezett „második összhang”. Hultsch szerint az első összhangot pedig úgy kapjuk meg, hogy a $100^{2}$-ét egy másik szám négyzetével megszorozzuk, és ez a szám: $36$, aminek a négyzete ($1296$) száz négyzetével megszorozva ismét $12\ 960\ 000$. Tehát így mindkét összhang ugyanazt a számot adja ki.
James Adam ismeri fel (1902-ben megjelent kommentárjában), hogy az epitritosz alap öttel összekapcsolva, háromszor sokszorozva [hatványozva] a következő:
$$(3 \cdot 4 \cdot 5) \cdot (3 \cdot 4 \cdot 5) \cdot (3 \cdot 4 \cdot 5) \cdot (3 \cdot4 \cdot 5) = (3 \cdot 4 \cdot 5)^4 = 12 960 000$$– ezek sorban: az első, a második és a harmadik sokszorozás.
Végül a $12\ 960\ 000$ rejtőzik a szöveg talányosabb első részében is.
Ennek megvilágítása Diès érdeme, aki felismerte a következő két összefüggést:
1. Aphrodisziaszi Alexandrosz (Arisztotelész, Metafizika 76, 20–26) szerint a püthagoreusok véleményének megfelelően az egyenlőtlen oldalú derékszögű háromszögben az átfogó $(5)$, az „uralkodó”, és a befogók $(3, 4)$ az „alávetettek” („dünamené” és „dünaszteiomenai”).
2. A „hasonlókból és nem hasonlókból származók” („homiúnta kai anomoiúnta”) a következők:
- „hasonlókból származó” – a kocka $(a \cdot a \cdot a = 3 \cdot 3 \cdot 3)$
- „nem hasonlókból származó” – a tégla $(a \cdot b \cdot c = 3 \cdot 4 \cdot 5)$
tehát „az emberi termékenységnek a száma, amelyben a ($3, 4, 5$ oldalú)
derékszögű háromszög átfogójának és befogóinak a sokszorozásai három
távolságot és négy határt [nagyságrendet] alkotnak:
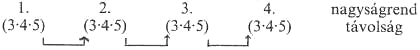
- „növesztők” és „fogyasztók” („auxanontész kai pthinontész”) –
ezt pedig a szöveg második részének a szavai értelmezik: „az egyik
úgy jön létre, hogy az egyenlőt egyenlővel és a százat százzal
megszorozzuk”:
$$x^{2} \cdot 100^{2}; \ 36^{2} \cdot 100^{2} = 12\ 960\ 000$$ $$x^{2} = 36^{2} = (3 \cdot 3 \cdot 4) \cdot (3 \cdot \color{red}3 \cdot \color{red}4) \text{ növesztők}$$ $$100^{2} = (5 \cdot 5 \cdot 4) \cdot (5 \cdot \color{red}5 \cdot \color{red}4) \text{ fogyasztók}$$
Mindebből láthatjuk, hogy a kérdéses szám mindenképpen $12\ 960\ 000$, amelyet Platón számos különböző tényezőre bont szét; ezek közül különös jelentősége van a $3,4,5$-nek. A $3,4,5$ egységoldalú derékszögű háromszöget a püthagoreusok különösen jelentősnek tartották.
És vajon az alább olvasható végkövetkeztetés már a „gondolta a fene” kategóriájába sorolható? – A szerk.
Vajon miért olyan fontos ez a szám a nemzések időpontjának megjelölésében? $12\ 960\ 000$ perc az kb. 25 évet tesz ki. Ebben az életkorban kezdhetik meg Platón szerint a férfiak a nemi életet. $12\ 960\ 000$ nap az kb. $36\ 000$ év, a babiloni világév, amelynek keretén belül egy világkorszak lezajlik.
