Bevezetés
A változó áttételű, nem kör gördülő görbéjű fogaskerekek a hajtástechnika méltatlanul kevéssé ismert, ritkán használt gépelemei. Az elmúlt évszázadok logarléccel, körzővel-vonalzóval dolgozó mérnökei még bátran alkalmazták ezeket az érdekes alkatrészeket. A szerszámgépek előtoló mechanizmusaiban, az elektromechanikus számítógépek függvény generátorainak potenciométereiben, a nyomda, textil és élelmiszeripar megannyi berendezésében működő nemlineáris centrois mechanizmusok mára csaknem teljességgel eltűntek a gyakorlatból.
A vezérelt villamos hajtások fejlődése némiképpen magyarázza e különleges gépelemek háttérbe szorulását. A változó áttételű fogaskerék hajtás a periodikusan gyorsuló-lassuló mozgások előállítására azonban
- csupán két mechanikus elemet igényel,
- egyszerű alakú,
- jól terhelhető,
- megbízható, hosszú élettartamú szerkezet.
A mérnöki munkát segítő számítógépi rendszerek (CAD-CAM és szimbolikus matematikai programok) és az új technológiák (huzalszikra forgácsolás, rapid prototyping eljárások, koordináta méréstechnika) a szabatos tervezés, gyártás és ellenőrzés minden szükséges lehetőségét biztosítják – ám a legegyszerűbb elliptikus fogaskerékpár létrehozásához szükséges alapismeretek nem lelhetők fel műszaki felsőoktatásunk egyetlen, ma oktatott tantárgy tematikájában sem.
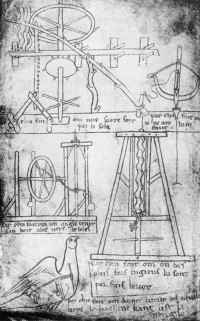
A jelen összeállítás a változó áttételű fogaskerekek egy különleges változatát vizsgálja. A kör alakú, excentrikusan csapágyazott fogaskerékkel kapcsolódó ellenkerék sajátos alakja Leonardo da Vinci Madridi Kódex című vázlatgyűjteményében található [7]. A cikk e különleges – ismereteink szerint a szakirodalomban eddig nem vizsgált – hajtáspár tervezésének és gyártásának kérdéseit tárgyalja.
Leonardo fogaskerekei
Leonardo da Vinci, a nagy reneszánsz művész civilizációnk mindmáig ható, emblématikus alakja. Festményei a leghíresebb múzeumok féltve őrzött kincsei, neve a komoly nemzetközi tudományos projektek, a könyv és filmpiac legfrissebb bestseller címei között egyaránt fellelhető. Titokzatos személyisége, torzójában is monumentális életműve megannyi ellentmondó értelmezésre, túl- és alulértékelésre egyaránt alapot szolgáltat. A róla szóló könyvtárnyi kommentárirodalomban olykor minden idők legnagyobb polihisztora, máskor zseniális dilettáns – személye néha különleges küldetésű kiválasztott, más elemzőnél naiv álmodozó. Elképesztő részletességű, gyönyörű vázlatain meglepően modern benyomást keltő szerkezetek, precíz anatómiai ábrák és monumentális épületek, fényképszerűen pontos állat- és emberalakok, a jövő futurisztikus városának és pusztító háborújának képei burjánzanak. Matematikai tárgyú feljegyzéseiben az alapműveletek eredményei sokhelyütt hibásak, másutt azonban az évszázadokkal később felfedezett integrálszámítás alapjai sejlenek fel.
A XV–XVI. század fordulóján az alkalmazott mechanikai és technológiai ismeretek már meglepően fejlettek voltak. Jóllehet a korabeli tudomány szempontjából nem tartoztak a disciplináris értékek közé, a katonai és civil célokra készült, megvalósult vagy csak elképzelt gépszerkezetek már számos olyan konstrukciós elemet tartalmaztak, amelyek mérnökhallgatóink tananyagában és napjaink műszaki alkotásaiban egyaránt helyet kapnak – avagy oda bátran beilleszthetők lennének. Az ókortól ismert egyszerű fizikai elemek (lejtő, csavar, emelő, hengerkerék, csigasor) mellett a – technika- és kultúrtörténeti szempontból méltatlanul kevéssé elemzett – karos-csuklós, valamint centrois (bütykös és fogaskerék) mechanizmusok több változatát már ismerték és alkalmazták. A könyvnyomtatás felfedezése révén nagyobb példányszámban válhattak közkinccsé a műszaki ismeretek. Az ókori,1 majd a középkorban2 élt alkotók sok századon keresztül, kézzel másolt alapkönyvei után a korabeli3 szerzők munkái is segítették a tudás terjedését.
A kerekes óra egy szép versszaknyi terjedelemben már Dante XIV. században írott Isteni színjátékában említésre került.4 A spanyol népköltészetben mindmáig él a toledói mechanikus vízemelő csodagépet megalkotó Juanelo Turriano,5(1) a „hispániai Faust” legendás alakja. A nem sok évvel Leonardo után alkotó nagy mérnökök6 szépen illusztrált kötetei a korabeli technika fejlettségét bizonyítják.
A kinematikai szabadságfok kérdésköre csak a XIX–XX. századfordulóra tisztázódott. A XV–XVI században még hiányzó matematikai apparátus miatt a szerkezeti méretek, arányok olykor irreálisak – Leonardo „naiv” műszaki érzéke és lenyűgöző térlátása azonban egyetlen, mégoly bizarr készülékénél sem vétett lényeges, elvi, a működőképességet befolyásoló hibát. [11] Az excentrikus, kör gördülő görbéjű evolvens fogaskerék ismert alakja a Reauleaux féle kinematikai gyűjteményben szerepel. A szakirodalomban Litvin alapművei [1–4] részleteiben is tárgyalják e fogaskerék rendszer legfontosabb sajátosságait. A profiltervezés komplex algebrai módszerével kapcsolatban lásd az [5–6], illetve [8] forrásokat.
A jelen összeállítás szerzője Leonardo Madridi Kódex címen ismert vázlatgyűjteményében bukkant a változó áttételű fogaskerék hajtások néhány vázlatára. Az 1(a) ábra szembeszökően nagy excentricitású, kör alakú fogaskerekei, valamint a vázlatgyűjtemény további lapjain (például 1(b) ábra) látható szerkezetek alapján egyértelmű, hogy Leonardo a gyorsuló-lassuló forgó mozgás átvitelének lehetőségeit is kereste. Az 1(a) ábra jelölt konstrukciója szabályos kör alakú kerekekkel bár nem valósítható meg, a körhöz közeli, kis excentricitású ellipszis fogaskerekekkel azonban működőképes. A kör alakú, excentrikus kerékkel kapcsolódó ellenkerék 1(b) ábra kiemelt alakja egy különleges érdekességű szerkezetet eredményez.
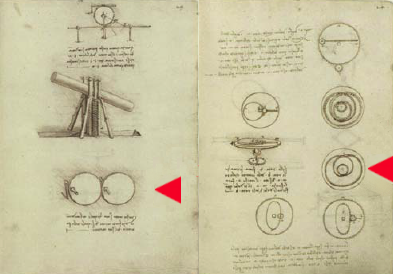
a. b. Cams. Madrid MS I, f. 28 v
A fogazatok gördülő görbéi
A kör alakú kereket $z$, a nem kör alakú ellenkereket $z,2z,\dots,nz$ fogszámmal kialakítva a hajtás globálisan állandó, vagy lassító áttételű. Vagyis a kör alakú fogaskerék egy teljes fordulatára az ellenkerék $1,\dots,1/n$ teljes fordulatot végez. (A kör alakú kerék egy körülfordulása során megvalósuló lassító-gyorsító mozgásciklus a nem kör alakú kerék egy teljes körülfordulása során $1, 2, \dots, n$ alkalommal jön létre.)
A – meglehetősen gyér – nemzetközi szakirodalomban is teljességgel ismeretlen az excentrikus, kör alakú kerékkel kapcsolódó, globálisan gyorsító fogaskerék. Ennél a rendszernél a kör alakú fogaskerék egy teljes fordulatára az ellenkerék $2,3,\dots,n$ teljes körülfordulása adódik. Az excentrikus, kör alakú kerékkel kapcsolódó ellenkerék gördülő görbéjének meghatározásához elsőként írjuk fel a kör alakú kerék gördülő görbéjének polár egyenletét.
A polár koordináta rendszer kezdőpontját helyezzük az $O_{1}C_{1}=e$ excentricitású, $C_{1}P_{1}=a$ osztókör sugarú kerék forgáspontjába. A 2(a) ábra a kerék alaphelyzetét, a 2(b) ábra a kezdetihez képest $C_{1}OP_{1}=C_{2}OP_{2}=\phi$ szöggel elfordult helyzetét szemlélteti:
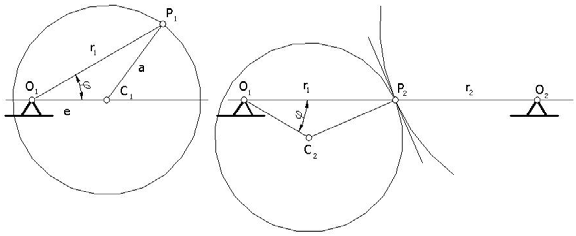
A $C_{1}O_{1}P_{1}$ háromszögre felírt cosinus tétel az $O_{1}P_{1} = r_{1}$ jelöléssel
$${a}^{2}={e}^{2}+{r}_{1}^{2}-2e{r}_{1}\cos\phi\tag{1}$$illetve – az $r_{1}$ ismeretlenre másodfokú egyenlet két megoldásából a pozitív diszkriminánst választva
$${r}_{1}=\sqrt{{a}^{2}-{e}^{2}{\sin^{2}\phi}}+e\cos\phi\tag{2}$$A kör alakú kerékkel kapcsolódó ellenkerék tengelytávolsága legyen az egyelőre ismeretlen $O_{1}O_{2}=E$. A kör alakú kerék $r_{1}$ sugarú gördülőköri pontjával nyilván az ellenkerék
$${r}_{2}=E-{r}_{1}\tag{3}$$sugarú pontja kapcsolódik.
A gördülő görbék egymáson csúszás nélkül gördülnek. A pillanatnyi érintkezési helyzethez tartozó polársugaraik aránya a $\xi$ áttételi függvény. (Az áttételi függvény egyben a 2 indexű, nem köralakú hajtott és az 1 indexű, kör alakú hajtó fogaskerék szögsebességeinek aránya.)
$$\xi =\frac{{r}_{1}}{{r}_{2}}=\frac{{\omega }_{2}}{{\omega }_{1}}\tag{4}$$Az 1 kerék $\phi$ polárszöghöz tartozó kapcsolódási helyzetére az áttételi függvény
$$\xi =\frac{\sqrt{{a}^{2}-{e}^{2}{\sin(\phi)}^{2}}-e\cos(\phi)}{E-\sqrt{{a}^{2}-{e}^{2}{\sin(\phi)}^{2}}+e\cos(\phi)}\tag{5}$$Határozzuk meg a $E$ tengelytávolságot olyképpen, hogy a kör alakú hajtó kerék egy fordulata során a hajtott, nem kör alakú kerék pontosan két teljes fordulatot végezzen. Legyen a hajtó szögsebesség $\omega_{1} = 1$. Az áttételi függvényt a $\phi=[0..\pi]$ tartományban (a hajtó kerék fél fordulata során) integrálva a hajtott kerék egy teljes fordulata adódik:
$$\underset{0}{\overset{\pi}{\int}}\xi d\phi=2\pi\tag{6}$$Az egyenlet kifejtett alakja:
$$\xi =\frac{\sqrt{{a}^{2}-{e}^{2}{\sin(\phi)}^{2}}-e\cos(\phi)}{E-\sqrt{{a}^{2}-{e}^{2}{\sin(\phi)}^{2}}+e\cos(\phi)}\tag{7}$$A (7) egyenletből az $E$ érték zárt alakban nem fejezhető ki, azonban az $e$ és az $a$ paraméterek konkrét értékeivel, például az intervallum felezés gyökközelítő módszerét alkalmazva könnyen meghatározható.
Az áttételi függvény értelmezéséből következően a hajtó kerék $\lambda$ szögű elfordulásához a hajtott kerék
$$\kappa =\underset{0}{\overset{\lambda}{\int }}\xi d\phi\tag{8}$$szögű elfordulása tartozik. A hajtott kerék ezen kapcsolódási helyzetében a polársugár értéke
$${r}_{2}={r}_{2}(\phi=\lambda)\tag{9}$$A hajtott kerék forgáspontjával egybeeső origójú derékszögű koordináta rendszerben az $r_{2}(\phi=\lambda)$ polársugárhoz tartozó görbepont $x, y$ koordinátái:
$$x={r}_{2}\cos\kappa\enspace\enspace y={r}_{2}\sin\kappa\tag{10}$$A bemutatott összefüggéseket alkalmazva, $e=20, a=48$ esetben a (7) egyenlet egyik numerikus megoldására $E=99,9596038$ értéknél a hajtott kerék gördülő görbéjének szokványos, míg az $E=79,86777595$ értékre a Leonardo-vázlaton láthatóhoz hasonló, önátmetsző alakzata adódik (3. ábra):
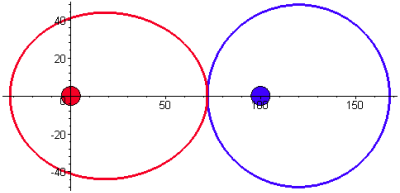
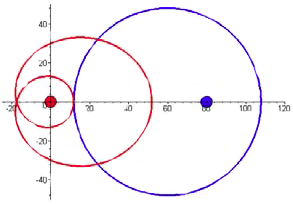
A kerekek fogazatai
A gördülő görbék alapján könnyűszerrel előállítható a Leonardo elképzelése szerinti pálcás fogaskerék valamint a kapcsolódó ciklois profilú homlokkerék CAD modellje (4. ábra):

(A pálcás és ciklois fogazattal kapcsolatban lásd a [2–4], illetve a [9–10] forrásokat.)
Az önátmetsző gördülő görbéjű fogaskerék megvalósítható, ha az önmetszési ponttól balra, illetve jobbra eső fogazatot a forgástengely irányában eltolt, párhuzamos síkokban hozzuk létre. A folyamatos forgó mozgást biztosító fogazatnál a gördülő görbe önátmetszési pontja egy fogárok (vagy fog) középpontjával esik egybe.
A hajtott kerék egy teljes, n radián mértékű elfordulásához a hajtó kerék $e$ szögű elfordulása tartozik. A korábbiakkal összhangban
$$\underset{0}{\overset{\theta}{\int}}\xi d\phi=\pi\tag{11}$$vagyis az (önátmetsző gördülő görbéjű) ellenkerék és az excentrikus kör alakú hajtókerék elfordulásának aránya megegyezik az ellenkerék $z(\theta)$ és a hajtókerék $z(\pi)$ fogszám arányával.
$$i=\frac{\theta}{\pi}=\frac{\mathrm{z}(\theta)}{\mathrm{z}(\pi)}\tag{12}$$Az i értékét elemi lánctört sorozattal felírva, az ötödik $\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{8}}}}$ közelítés 7 tizedesjegyre pontos értéke $i=35/44$.
Vagyis az excentrikus, kör alakú kerék fogszámát $z_{1}=88$-ra, az önátmetsző gördülő görbéjű ellenkerék fogszámát $z_{2}=44$-re választva az alaphelyzetből induló rendszer a $z_{12}=35$-ik fogpár kapcsolódásnál jut el az önátmetszési pontig.
A (4) áttételi függvényt az $\omega_{1}=1$ szögsebességgel működő hajtókerékhez felrajzolva, a hajtott kerék szögsebességének $\omega_{2}=0,56–5,8$ értékek között változik (5. ábra):

A kerekeket a klasszikus, $a=20^{\circ}, h=1, c=0,25$ alakjellemzőjű evolvens fogazattal kialakítva, a modul az
$$m=\frac{2a\pi }{{z}_{1}}\tag{13}$$formulával $m=1,090909091$-re adódott.
A lefejtő lécprofil sarokponti komplex koordinátáit $Q_{j}$-vel jelölve, a (9.) gördülő görbén csúszás nélkül legördített léc $j$ indexű sarokpontjának komplex koordinátái:
$${w}_{j}=({Q}_{j}-L){e}^{i(\phi+\mathrm{\mu}(\phi))}+{r}_{2}{e}^{i\phi}\tag{14}$$ahol
$$\mathrm{\mu}(\phi)=\arctan\left[\frac{{r}_{2}}{\frac{d{r}_{2}}{d\phi}}\right] \enspace\enspace L=\underset{0}{\overset{\phi}{\int}}\sqrt{{r}_{2}^{2}+{\left[\frac{d{r}_{2}}{d\psi }\right]}^{2}}d\psi\tag{15}$$$\mu(\phi)$ a (9.) görbe polársugara és érintője által bezárt szög, illetve $L$ a (9.) görbén csúszás nélkül legördült szerszám gördülő egyenesének hossza.
A fogazatok tervezéséhez a Maple V. R10 és az AUTOCAD 2002 programokat használtuk. A működőképes szerkezet a BME Gépgyártástechnológia Tanszék ragasztott papír rétegekkel dolgozó (LOM) gyors prototípus gyártó berendezésén készült el (6. ábra):


Összefoglalás
A cikk Leonardo da Vinci néhány, a Madridi Kódex gyűjteményben fellelhető fogaskerék vázlata nyomán az excentrikus, kör alakú fogaskerék kapcsolódását vizsgálja. A tengelytáv alkalmas megválasztásával az ellenkerék sajátos, önátmetsző gördülő görbéje adódik. A kerekek kapcsolódó fogszámait és evolvens fogazati jellemzőit meghatározva, a rapid prototyping technológiával legyártott hajtáspár – közel 600%-os max. áttételi viszony mellett – teljességgel működőképesnek bizonyult.