1783. szeptember 18-án Szentpéterváron Leonhard Euler napja ugyanúgy kezdődött, mint máskor. Matematikaórát tartott egyik unokájának, majd belekezdett egy számításba a léghajók repülésével kapcsolatban. Éppen három hónappal korábban, Lyontól délre a Montgolfier testvérek egy hatalmas léghajót bocsátottak fel, amely majdnem kétszáz méter magasságig emelkedett fel, majd körülbelül egy mérfölddel arrébb biztonságosan földet ért. Euler a léghajó mozgásának mechanikáján dolgozott, amikor a Montgolfier testvérek XVI. Lajos előtt Párizsban egy birkát készültek felvinni a levegőbe. A repülés szeptember 19-én lezajlott. Euler azonban már nem hallhatott róla. Ebéd után asszisztensével az akkoriban felfedezett Uránusz bolygó pályájának kiszámításán dolgozott. A bolygó különös pályáját leíró, általa bevezetett egyenletek évtizedek múlva majd a Plútó bolygó felfedezéséhez vezetnek. Euler nem lehetett tanúja ennek a felfedezésnek sem. Délután öt óra tájban agyvérzést kapott, és azt suttogta, „meghalok”, mielőtt elveszítette eszméletét. Azon az estén meghalt, bevégezve minden idők legtermékenyebb matematikai karrierjét.
A svájci születésű Euler, aki élete nagy részét Berlinben és Szentpéterváron töltötte, különösen nagy hatást gyakorolt a matematika minden területére, a fizikára és a mérnöki tudományokra. Nemcsak felfedezéseinek fontossága, már puszta mennyisége is lenyűgöző. Az Opera Omnia, Euler – még nem teljes – összegyűjtött munkáinak jegyzéke jelenleg több mint 73 kötetből áll, amelyek mindegyike hatszáz oldalas. Euler életének utolsó 17 éve, amely 1766-os szentpétervári visszatérésétől 76 éves korában bekövetkezett haláláig tartott, eléggé viharos volt. A sok személyes tragédia ellenére műveinek közel felét ezekben az években írta. Ezek közé tartozik a Hold mozgását leíró, hétszázhetvenöt oldalas értekezése, egy nagy hatású algebrakönyv, valamint az integrálszámítás háromkötetes kifejtése, amelyet úgy fejezett be, hogy közben átlagban heti egy matematikai cikket jelentetett meg a szentpétervári akadémia lapjában. A meglepő ebben az, hogy ebben az időben sem olvasni, sem írni nem volt már képes: 1766-os szentpétervári visszatérése után hamarosan részlegesen elveszítette látását, és egy 1771-ben végzett sikertelen hályogműtét következtében végleg megvakult. A tételek oldalainak ezreit mind fejből diktálta.
Három évtizeddel korábban, még szeme világának birtokában, Euler írt egy rövid cikket egy szórakoztató problémáról, amely a szentpétervári otthonától nem messze lévő Königsbergből származott. Königsberg ebben az időben virágzó kelet-poroszországi város volt, és senki nem sejthette, hogy milyen szomorú sors vár rá a második világháború egyik legádázabb csatájának színhelyeként. A korabeli rézkarcok egy, a Pregel partjain elterülő, gyorsan fejlődő várost ábrázolnak, ahol serény hajók flottája és a velük folytatott kereskedés kényelmes életet biztosított a helyi kereskedőknek és családjaiknak. A prosperáló gazdaság lehetővé tette a város elöljárói számára, hogy nem kevesebb mint hét hidat építsenek a folyón. Ezek többsége az egyes városrészeket kötötte össze az elegáns Kneiphof-szigettel, amely a Pregel két ága közé ékelődött. Két másik híd a folyó két ágát keresztezte (1.1 ábra). A békében és jólétben élő königsbergiek fejtörőkkel szórakoztak. Az egyik például így szólt: „Átsétálhatunk-e a hét hídon úgy, hogy közben egyiken se megyünk át kétszer?” Senki nem tudott ilyen útvonalat találni, egészen addig, míg 1875-ben egy új hidat nem építettek.

Königsberg elrendezése 1875 előtt a Kneipfhof-szigettel (A) és a Pregel folyó két ága közötti D földterülettel. A königsbergi probléma megoldása azt jelentette, hogy a város körül olyan útvonalat találjunk, ami egy személytől minden egyes hídon csak egyszeri átkelést igényelne. 1736-ban Leonhard Euler létrehozta a gráfelméletet azáltal, hogy a négy földterület mindegyikét pontokkal (A-tól D-ig) és minden egyes hidat pedig egy éllel (a-tól g-ig) helyettesített, amellyel egy négy pontból és hét élből álló gráfot kapott. Aztán bebizonyította, hogy a königsbergi gráfon nem létezik olyan útvonal, amelyik minden élt csak egyszer metsz.
1736-ban, majdnem 150 évvel az új híd megnyitása előtt, Euler egzakt matematikai bizonyítást adott arra, hogy az akkor meglévő hét hídon át ilyen útvonal nem létezik. Azon túl, hogy megoldotta a königsbergi problémát, rövid cikkében tudtán kívül is útjára indította a matematika egy csodálatosan gazdag ágát, a gráfelméletet. Ma a hálózatokról való gondolkodásunk alapja a gráfelmélet. Az Eulert követő évszázadok alatt a gráfelmélet fejlődéséhez a legnagyobb matematikusok járultak hozzá. Mielőtt a hálózatok ajtajának világát kitárnánk, pillantsunk bele röviden abba a gondolatmenetbe, amely Eulert az első gráfok bevezetésére indította.
1.
Euler bizonyítása egyszerű és elegáns, könnyen megértheti az is, aki matematikailag nem képzett. Viszont mégsem a bizonyítás vonult be a történelembe, hanem inkább a probléma megoldásához felhasznált közbülső lépés. Euler nagyszerű meglátása abban rejlett, hogy a königsbergi hidakat gráfoknak tekintette: olyan pontoknak, amelyeket élek kapcsolnak össze. Ehhez a folyó által egymástól elválasztott négy földterületnek megfeleltetett négy pontot, és ezeket A, B, C és D betűkkel jelölte. Aztán a hidakat éleknek nevezte el, és vonalakkal kötötte össze azokat a földdarabokat, amelyek között híd volt. Így egy gráfot kapott, amelynek pontjai a földdarabok voltak, élei pedig a hidak.
Euler bizonyítása egy egyszerű megfigyelésen alapult. Minden páratlan számú éllel rendelkező pont vagy kezdő-, vagy végpontja kell, hogy legyen az útvonalnak. Minden hídon áthalad egy folytonos útvonal, amelyiknek csak egy kezdő- és egy végpontja lehet. Ezért ilyen útvonal nem létezhet olyan gráfon, amelynek több mint két, páratlan számú éllel rendelkező pontja van. Mivel a königsbergi gráfnak négy ilyen pontja volt, ezért nem is találhatott volna senki a feltételeknek megfelelő útvonalat.
Számunkra Euler bizonyításának legfontosabb része az, hogy az útvonal léte nem a mi leleményességünkön múlik. Ez a gráf belső tulajdonsága. A königsbergi hidak korabeli elhelyezése esetén, függetlenül attól, hogy milyen leleményesek vagyunk, a kívánt útvonalat nem találhatjuk meg. A königsbergiek végül egyetértettek Eulerrel és feladták a reménytelen keresést. 1875-ben a B és C terület között új hidat építettek, ezzel megnövelve e két pont éleinek számát. Most már csak két pont (A és D) maradt páratlan számú éllel, és egyszerű volt a kívánt útvonalat megtalálni. Lehet, hogy ennek az útvonalnak a létrehozása volt a híd felépítésének rejtett indítéka?
Visszapillantva, Euler nem szándékos üzenete nagyon egyszerű. A gráfok és hálózatok tulajdonságai a felépítésükben rejlenek, és segítenek vagy hátráltatnak minket abban, hogy az adott hálózat segítségével valamit végrehajtsunk. Több mint két évszázadon keresztül a königsbergi gráf szerkezete nem engedte, hogy a polgárok kávéházi feladványukat megoldják. De ha egy él hozzáadásával megváltoztatjuk a gráf felépítését, ez a korlátozás hirtelen megszűnik.
Euler eredménye sokféleképpen szimbolizálja e könyv üzenetét. A minket körülvevő összetett világ megértésének kulcsa a gráfok vagy hálózatok felépítése és szerkezete. A csak kevés pontra vagy élre ható, a topológiában végrehajtott kis változások rejtett ajtókat tárhatnak ki, és ezek nyomán új lehetőségek keletkezhetnek.
A gráfelmélet Euler után olyan matematikai óriások hozzájárulásával lendült fel, mint Cauchy, Hamilton, Cayley, Kirchhoff és Pólya. Ők fedeztek fel majdnem mindent, ami napjainkban az olyan nagy, rendezett gráfokkal kapcsolatban ismert, mint amilyen az atomokból kialakuló kristályrács, vagy a méhkaptárakban a méhek által készített hatszögletű rács. A XX. század közepéig a gráfelmélet célja egyszerű volt. A különböző gráfok tulajdonságait kívánta feltárni és katalogizálni. A híres problémák közé tartozott, hogy megtaláljuk a menekülési útvonalat egy labirintusból; ezt először 1873-ban oldották meg. Ilyen volt a sakktáblán annak a lépéssorozatnak a megtalálása, amivel a ló minden mezőt egyszer érint, és visszatér kiinduló pontjába. Volt néhány nehéz probléma is, amely évszázadokon keresztül megoldatlan maradt.
Kétszáz évnek kellett eltelnie Euler gondolatébresztő munkája óta, míg a matematikusok áttértek a különféle gráfok tulajdonságainak tanulmányozásáról arra a lényeges kérdésre, hogyan jönnek létre a gráfok, vagy általánosabban: a hálózatok. Valóban, hogyan alakul ki egy valódi hálózat? Milyen törvények irányítják megjelenésüket és szerkezetüket? Ezek a kérdések és az első válaszok 1950-ig várattak magukra, amikor két magyar matematikus forradalmasította a gráfelméletet.
2.
Az 1920-as évek végének Budapestjén egy különös mozgású, 17 éves ifjú vágtázott az utcákon, és megállt egy elegáns cipőbolt előtt, ahol mérték után készített cipőket árultak. Furcsa formájú lábával, amelyre normális cipő soha nem illett volna, valóban jó hasznát vette volna egy cipésznek. Látogatásának oka azonban nem egy új cipő volt. Bekopogtatott a bolt ajtaján, majd belépett és – nem törődve az eladónővel a pultnál – odament a bolt hátsó részében lévő 14 éves fiúhoz. Ez a viselkedés akkor is épp olyan furcsának tűnt, mint amilyennek ma tűnne.
– Mondj egy négyjegyű számot! – mondta.
– 2532 – jött a tágra nyitott szemű fiú válasza, ahogy rámeredt a furcsa alakra. Az idősebb fiú azonban nem hagyta őt túl sokáig bámulni.
– A négyzete 6 441 024 – folytatta. – Elnézést, öregszem, és nem tudom megmondani a köbét. Hány bizonyítását ismered a Pitagorasz-tételnek?
– Egyet – válaszolta a fiatalabb.
– Én harminchetet tudok – folytatta anélkül, hogy levegőt vett volna. – Tudtad, hogy egy egyenes pontjainak halmaza nem megszámlálható?
Miután az éles eszű fiú megmutatta Cantor bizonyítását, és végzett teendőjével a cipőboltban, így szólt:
– Sietek – és így is tett, sarkon fordult és kivágtatott a boltból.
Erdős Pál továbbvágtázott, és a XX. század legnagyobb zsenije és leghíresebb különce lett belőle. 1996-ban bekövetkezett haláláig több mint 1500 matematikai cikket írt. Ez az Euler óta páratlan életmű tartalmazza egy másik magyar matematikussal, Rényi Alfréddal közösen írt nyolc cikkét. Ez a nyolc cikk a történelem folyamán először tette fel a legalapvetőbb kérdést gazdagon összekötött világunkról: milyen módon jönnek létre a hálózatok? Megoldásuk lefektette a véletlen hálózatok elméletének alapjait. Ez az elegáns elmélet olyan mélyen meghatározta gondolkodásunkat a hálózatokról, hogy még ma is nehezen tudunk tőle elszakadni.
3.
Válassz száz embert, akik közül egyik sem ismeri a másikat, és hívd meg őket koktélpartira. Ha megkínálod ezeket az idegeneket borral és sajttal, rögtön beszélgetni kezdenek, hiszen a találkozás és a mások megismerésére irányuló alapvető emberi vágy mindig összehozza az embereket. Hamarosan harminc-negyven, egyenként két vagy három emberből álló csoport jön létre. Ezután említsd meg az egyik vendégnek, hogy a címkézetlen sötétzöld üvegben lévő vörösbor egy ritka, húszéves, kiváló minőségű portói; sokkal jobb, mint a vörös címkés. De kérd meg ezt a vendéget, hogy csak ismerőseivel ossza meg ezt az információt. Tudod, hogy a drága portói eléggé biztonságban van, mert barátodnak csak két vagy három emberrel volt ideje a szobában találkozni. A vendégek azonban elkerülhetetlenül elunják magukat, ha túl hosszú ideig ugyanazzal az emberrel beszélgetnek, és ilyenkor továbbmennek, hogy egy másik csoporthoz csatlakozzanak. Egy külső megfigyelő semmi különöset nem venne észre. Mégis láthatatlan személyes kapcsolat van azok között, akik korábban találkoztak, de most különböző csoporthoz tartoznak. Emiatt szövevényes szálak kezdik összekötni azokat az embereket is, akik eddig még nem találkoztak. Például, Mari ugyan még nem találkozott Jánossal, de mindketten találkoztak Mikivel, és így Jánostól Mariig Mikin keresztül vezet egy útvonal. Ha János tudott a borról, valószínűleg most már Mari is tud róla, mivel hallhatott róla Mikitől, akinek János beszélt róla. Ahogy telik az idő, a vendégeket egyre növekvő mértékben láthatatlan kapcsok kötik össze, az ismeretségek finom hálója alakul ki, amely a vendégek nagy részét magában foglalja. A drága bor egyre inkább veszélybe kerül, ahogy híre a beavatottak kis csoportjától egyre több beszélgető csoporthoz jut el (1.2 ábra).
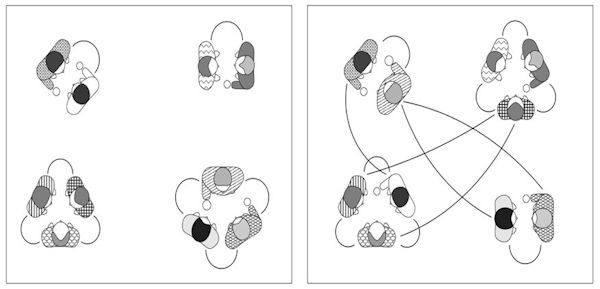
Egy tíz vendégből álló partin, ahol senki sem ismerte a másikat korábban, ismeretségi kapcsolatok alakultak ki, ahogy a vendégek kis csoportokban elkezdenek egymással fecsegni. Először a csoportok egymástól elkülönülnek (bal oldali ábra). Bár létezik azok között ismeretségi kapcsolat (folytonos vonal jelöli), akik egy csoportban vannak, a csoporton kívül még mindenki idegen. Ahogy múlik az idő (jobb oldali ábra), három vendég különböző csoportokhoz megy át, és egy óriáscsoport jön létre. Bár nem mindenki ismer mindenkit, most már egyetlen ismeretségi hálózat van, amely magában foglalja az összes vendéget. Ahogy követjük az ismeretségi kapcsolatokat, tetszőleges két vendég között most van útvonal.
Feltéve, hogy minden személy továbbadja az információt minden új ismerősének, elér-e a parti végére a kiváló portói híre minden vendéghez? Biztosak lehetünk abban, hogy ha mindenki ismerné egymást, akkor mindenki a címkézetlen üvegből öntögetné a jobb bort. Ha azonban minden találkozás akár csak tíz percig tart, akkor a 99 másik emberrel ez nagyjából 16 órát venne igénybe. A koktél partik ritkán tartanak ilyen hosszú ideig. Ezért gondolhatod úgy, hogy a barátodnak elárulhatod a titkot, és jó esélyed van arra, hogy a koktélparti végére is marad még a borból.
Erdős Pál és Rényi Alfréd mert másképpen gondolkodni. „A matematikus olyan gép, amely a kávéból tételt csinál” – szokta Erdős mondani, Rényit idézve. Az egyik különösen jól sikerült csésze kávé egy sokat idézett tétellé változott. Ha minden ember legalább egy másik vendéggel megismerkedik, akkor hamarosan mindenki a félretett portóit issza majd. Erdős és Rényi szerint harminc perc alatt kialakulna egy olyan láthatatlan ismeretségi hálózat, amely az összes vendéget magában foglalja. Könnyen előfordulhat, hogy néhány perccel azután, hogy a jó borról hallunk, már csak egy üres üveget találunk a helyén.
4.
A vendégek, akikkel az iménti koktélparti során találkoztunk, részét alkotják egy olyan problémának, amely a matematika Euler által felfedezett ágához, a gráfelmélethez tartozik. A vendégek a gráf csúcspontjai, és minden találkozás egy kapcsolatot hoz létre. Így keletkezik az ismeretségi hálózat (egy gráf): pontok élekkel összekötve. A telefonvonalakkal összekötött számítógépek, testünk molekulái biokémiai reakciókkal összekapcsolva, cégek és vevők, akiket a kereskedelem köt egymáshoz, az axonokon keresztül kapcsolódó idegsejtek, hidakkal összekötött szigetek – mind példák a gráfokra. Mindegy, hogy pontosan mit jelölnek a pontok és a közöttük lévő kapcsolatok, a matematikus számára ugyanazt jelentik: egy gráfot, vagy más néven hálózatot.
Elegáns megoldásnak tűnhet, de minden hálót egyszerűen gráfként kezelni elég félelmetes kihívást jelent. Miközben a társadalom, az internet, egy sejt, vagy az agy mind ábrázolható gráfokkal, mindegyikük nagyon különbözik a többitől. Nehéz sok közös vonást elképzelnünk az emberi társadalom és egy sejt között; az előbbiben barátokat és ismerősöket szerzünk véletlen találkozások és tudatos elhatározások egyvelege által, az utóbbiban pedig a kémia és a fizika érzelmektől mentes törvényei irányítják a molekulák közti összes reakciót. Kell, hogy legyen nyilvánvaló különbség a szabályok között, amelyek a természetben előforduló különböző hálózatokban a kapcsolatok elhelyezkedését irányítják. A sok különböző rendszer leírásának egy modellbe foglalása első ránézésre leküzdhetetlen kihívásnak tűnik.
Viszont minden tudós végső célja, hogy a nagyon összetett jelenségekre a lehető legegyszerűbb magyarázatot megtalálja. Erdős és Rényi elfogadta ezt a kihívást, és elegáns matematikai megoldást ajánlott az összetett gráfok közös keretben történő tárgyalására. Mivel a különböző rendszerek eltérő szabályokat követnek saját hálózatuk kialakításakor, Erdős és Rényi szándékosan figyelmen kívül hagyta a különbségeket, és előálltak a legegyszerűbb megoldással, ami a természet számára lehetséges: véletlenszerűen kötötték össze a pontokat. Úgy döntöttek, hogy a hálózat létrehozásának legegyszerűbb módja az, ha kockadobással döntenek. Válassz ki két pontot, és ha hatost dobsz, akkor helyezz el egy élt közöttük. Bármilyen más dobás esetén ne kösd össze a két pontot, hanem válassz egy másik párt és kezdd elölről. Erdős és Rényi ezért a gráfok és az általuk ábrázolt világ kialakulását alapvetően véletlenszerűnek látta.
„Van egy régi vita arról – szerette Erdős mondani –, hogy mi hozzuk-e létre a matematikát, vagy csak felfedezzük. Más szóval: ott rejtőzik-e valahol már az igazság, még ha mi nem is ismerjük azt?” Erdősnek volt egyértelmű válasza erre a kérdésre. A matematikai igazságok rajta vannak az abszolút igazságok listáján, és mi csak felfedezzük őket. A véletlen gráfok elmélete olyan elegáns és egyszerű, hogy számára az örök igazságok közé tartozónak látszott. Ma már tudjuk, hogy a véletlen hálózatok kis szerepet játszottak univerzumunk kialakulásában. A természet e helyett néhány alaptörvényt vett igénybe, amelyeket a következő fejezetekben fogunk bemutatni. Erdős maga alkotott matematikai igazságokat, és a véletlen gráfok elméletének kidolgozásával egy lehetséges látásmódot világunkról. Nem ismerte kellőképpen az emberi agyat és a társadalmat kialakító természeti törvényeket, és legjobb megoldási javaslata az volt, hogy könnyelműen azt feltételezte, Isten szeret kockázni. Princetonban dolgozó barátja, Albert Einstein az ellenkezőjéről volt meggyőződve: „Isten nem rulettezik a világegyetemmel.”
5.
Térjünk vissza a koktélpartihoz, és alkalmazzuk a véletlen gráfok elméletét. Induljunk ki sok elszigetelt pontból. Aztán véletlen módon a pontokhoz adjunk hozzá éleket, jelezve a vendégek közötti véletlen találkozásokat. Ha csak kevés élt alkotunk ily módon, akkor az egyetlen következmény az lesz, hogy néhány pont párt kap. Ha folytatjuk az élek létrehozását, elkerülhetetlenül összekapcsolunk majd egymással néhányat ezek közül a párok közül, és csoportokat alakítunk ki a különböző pontokból. De ha már annyi élt hozunk létre, hogy minden pontra átlagosan egy él jut, akkor megtörténik a csoda. Egyetlen hatalmas csoport (óriáscsoport) jelenik meg. Azaz, a legtöbb pont egy olyan csoport része lesz, amelyben egy tetszőleges pontból elindulva és az élek mentén navigálva bármelyik másik pontba eljuthatunk. Ez az a pillanat, amikor a drága bor veszélybe kerül, mivel a pletyka elér mindenkit, aki az óriáscsoporthoz tartozik. A matematikusok ezt a jelenséget az óriás komponens megjelenésének nevezik, amely komponens tartalmazza a pontok jelentős részét. A fizikusok perkolációnak hívják, és azt mondják, hogy éppen tanúi lettünk egy fázisátalakulásnak, olyannak, mint amikor a víz megfagy. A szociológusok azt fogják mondani, hogy egy közösség alakult ki. Bár a különböző tudományágak különböző elnevezéseket használnak, abban mindnyájan egyetértenek, hogy ha egy hálózatban véletlen módon választunk ki és kötünk össze pontpárokat, akkor valami különleges történik. A hálózat kritikus számú él elhelyezése után drasztikusan megváltozik. A változás előtt rengeteg pici, elszigetelt pontcsoportot látunk, emberek különálló csoportjait, akik a csoportokon belül kommunikálnak. A változás után pedig egy óriáscsoportunk lesz, amelynek majdnem mindenki része.
6.
Mindegyikünk egy nagy csoport része, a világméretű ismeretségi hálóé, amelyből senki nem marad ki. Senki sem ismer mindenkit a földön, de az garantált, hogy bármelyik két ember között e hálóban létezik elérési út. Hasonlóképpen, van útvonal agyunk tetszőleges két neuronja között, a világ bármelyik két cége között, testünk bármelyik két vegyi összetevője között. Semmi nincs kizárva az életnek ebből a szorosan összefüggő hálójából. Erdős Pál és Rényi Alfréd megmondta, miért: pontonként csak egyetlen élre van szükség, hogy összekapcsolva maradjunk. Személyenként egy ismerős, legalább egy összeköttetés agyunk minden egyes neuronjától egy másik neuronig, testünk mindegyik vegyi összetevőjének részvétele legalább egy kémiai reakcióban, kereskedés legalább egy vállalattal az üzleti világban. Egy a küszöbérték. Ha a pontoknak átlagban egynél kevesebb kapcsolata van, akkor hálózatunk kicsi, egymással nem kommunikáló csoportokra esik szét. Ha pontonként egynél több a kapcsolat, akkor ez a veszély nem fenyeget.
A természet újból és újból többszörösen túllépi a pontonkénti minimum egy kapcsolatot. A szociológusok úgy becsülik, hogy név szerint 200–5000 embert ismerünk. Egy átlag neuron több tucat másikkal áll kapcsolatban, néhányuk ezrekkel. Minden vállalat szükségszerűen eladók és vevők százaival van összeköttetésben; a legnagyobbak kapcsolatok millióival rendelkeznek. Testünkben a legtöbb molekula jóval több, mint egy kémiai reakcióban vesz részt, néhány, mint a víz is, több százban. A valódi hálózatok elemei tehát nem csupán össze vannak kapcsolva, a kapcsolatok száma jóval túllépi a minimális küszöböt. A véletlen gráfok elmélete szerint, ahogy az egy pontra jutó élek száma a kritikus egy fölé ér, az óriáscsoportból kimaradó pontok száma exponenciálisan csökken. Azaz, minél több élt adunk hozzá, annál nehezebb lesz elszigetelt pontot találnunk. A természet nem kockáztatja, hogy a küszöbhöz közel maradjon. Messze túllépi azt. Következésképpen, a körülöttünk lévő hálózatok nem egyszerűen csak hálók. Ezek sűrű hálózatok, amelyekből semmi nem menekülhet, és amelyeken belül minden pont elérhető. Emiatt ritka általában az embereknek a társadalomtól teljesen elkülönült szigete, és ezért tudjuk a testünket alkotó molekulákat egyetlen sejttérképen elhelyezni. Emiatt érte el Pál apostol üzenete azokat az embereket, akikkel soha nem találkozott, és ezért sikerült MafiaBoynak2 a címlapokra kerülnie. A kapcsolatokon keresztül tetteik könnyen hatottak milliókra.
7.
Óriási esemény volt a gráfelméletben, amikor Erdős és Rényi felfedezte azt a nagyon különleges pontot, ahol a fázis- vagy perkolációs átalakulás bekövetkezik, és egy óriási csoport bukkan fel. Nemcsak azért, mert ez azt a hihetetlen előrejelzést adta, hogy fejenként csak egy ismerősre van szükség egy társadalom kialakulásához, hanem főként azért, mert Erdős és Rényi előtt a gráfelmélet nem foglalkozott koktélpartikkal, ismeretségi hálózatokkal vagy véletlen gráfokkal. Majdnem kizárólag szabályos gráfokra koncentráltak, amelyeknek a szerkezetével kapcsolatban nem merült fel félreérthetőség. Amikor azonban olyan összetett rendszerekről van szó, mint az internet vagy az élő sejt, a szabályos gráfok inkább kivételesek, mint gyakoriak.
Erdős és Rényi először ismerte fel, hogy a valódi gráfok, a szociális hálózatoktól a telefonvonalakig, nem szépek és szabályosak. Reménytelenül bonyolultak. Miután rádöbbentek, hogy a valódi hálózatok szerkezete milyen bonyolult, a leíráshoz feltételezték, hogy véletlen hálózatokról van szó.
Visszapillantva nem meglepő, hogy ez a furcsa matematikus páros volt az, amelyik a véletlenszerűség bevezetésével a feje tetejére állította a matematika egy elismert ágát. A szerencse és a véletlen nagy szerepet játszott életükben. Bár Rényi 17 évvel fiatalabb volt Erdősnél, a szüleik közötti barátság révén még Budapestről ismerték egymást. Amikor 1948-ban Amszterdamban találkoztak és elkezdtek együtt dolgozni, már mindkettőjük mögött viharos évek álltak. Rényi a numerus clausus törvények miatt – amelyek korlátozták az egyetemre felvehető zsidók számát – egy hajógyárban dolgozott. Miután megnyert egy matematika és egy görög nyelvi tanulmányi versenyt, 1939-ben engedélyezték felvételét az egyetemre. Matematikai tanulmányainak befejezése után hamarosan behívták munkaszolgálatra, ahonnan valahogyan megszökött.
Erdős és kollégái, akik ismerték Rényi háború alatti ellenállási tevékenységét, mélyen csodálták és tisztelték őt. Egy történet szerint Rényi nyilas katonának öltözve bement a budapesti gettóba és sikerült szüleit onnan kihoznia. Évekig élt hamis papírokkal a nácik által ellenőrzött Budapesten. Csak azok tudták a tetteihez szükséges bátorságát igazán értékelni, akik jól ismerték a náci rémuralmat. Érthető, hogy Rényit mindez a háború végéig komolyan akadályozta abban, hogy a matematikára koncentráljon; ekkor 1946-ban Leningrádba utazott, hogy folytassa tanulmányait. Itt kreativitása segítségével csodákat művelt. Gyenge orosz nyelvtudása ellenére nemcsak megtanulta és rekordidő alatt magáévá tette a számelméletet, de annak közismerten nehéz problémájával, a Goldbach-sejtéssel kapcsolatban néhány alapvető tételt be is bizonyított. Így amikor két évvel később Amszterdamban Erdőssel találkozott, többé már nem csak ígéretes ifjú matematikus és családi barát volt, hanem nemzetközi elismertségű tudós.
Erdős addigra már kialakította a rá jellemző utazó matematikus életmódot. Feltűnt egy-egy kollégája ajtajában, és kijelentette: „elmém nyitott” – a matematikai igazság fáradhatatlan kereséséhez így szerzett társakat. Egyetlen állandó állásra kapott ajánlatot, Indiana államból, a South Bendben található Notre Dame Egyetemtől. Arnold Ross, a matematika tanszék akkori vezetője vendégprofesszori állást ajánlott Erdősnek, igen nagyvonalú feltételekkel. Akkor távozhat, amikor neki megfelel, hiszen az asszisztense folytatni tudja az előadásokat, amikor ő nincs ott.
A Notre Dame akkor még egy katolikus művészeti főiskola volt, nem az a neves egyetem, amivé évtizedek múlva vált. Mindamellett Erdősnek nyugodt és kényelmes munkakörnyezetet ajánlott, és lehetőséget a pap kollégákkal való gyakori beszélgetésekre. Erdős ezeket, az univerzummal és az istenséggel kapcsolatos sajátos látásmódja miatt, különösen élvezte. Amikor egyszer megkérdezték az ott töltött időről, visszafogottan megjegyezte, „túl sok a pluszjel”, amivel az egyetem területén található keresztekre utalt. Mikor végül a Notre Dame állandó állást ajánlott fel Erdősnek, hasonlóan kényelmes feltételekkel, ő udvariasan visszautasította. Valószínűleg túl nehéz lett volna elviselnie, hogy az életét jellemző véletlenszerűséget és váratlanságot elveszítse.
8.
Erdős és Rényi amszterdami találkozása egy szoros barátság és együttműködés kezdete lett, amely Rényi 1970-ben, 49 éves korában bekövetkezett korai haláláig több mint harminc közös cikket eredményezett. E publikációk között van a gráfelmélet nyolc legendás cikke. Az elsőben, amelyet több mint egy évtizeddel az amszterdami találkozó után publikáltak, először foglalkoztak azzal a fontos kérdéssel, hogyan alakulnak ki a gráfok. Az a megközelítés, ahogyan ők a gráfelméleti problémák kezelésére a véletlent felhasználják, akkor válik igazán világossá, ha megnézzük, hány éllel rendelkezik a gráf vagy hálózat egy-egy pontja. A szabályos gráfok abban kivételesek, hogy minden egyes ponthoz pontosan ugyanannyi él csatlakozik. Valóban, a merőleges egyenesekből álló kétdimenziós háló egy egyszerű négyzetrácsot alkot, minden pontjában pontosan négy éllel, a méhsejtek hatszögletű rácsában pedig minden pont három másikkal van összekötve.
Az ilyen szabályosság nyilvánvalóan hiányzik a véletlen gráfoknál. A véletlen hálózati modell alapgondolata a teljes esélyegyenlőség. Az éleket véletlenszerűen helyezzük el, és így az összes pontnak azonos az esélye arra, hogy megkapjon egy élt, pont úgy, mint Las Vegasban, ahol feltehetőleg mindnyájunknak egyforma az esélye a főnyeremény megnyerésére. Persze ennek ellenére a legtöbb játékostársunk szegényebben hagyja el az asztalt, mint mikor leült. Hasonlóképpen, ha véletlenszerűen helyezzük el a gráfban az éleket, akkor egyes pontokhoz több él tartozik majd. Néhányuknak meg pechjük is lehet, és egy ideig nem kapnak semmit. Erdős és Rényi véletlen világa egyszerre lehet tisztességtelen és nagylelkű. Valakiből szegényt, másokból gazdagot csinál. Viszont az Erdős–Rényi-elmélet hosszú távú előrejelzése szerint ez csupán látszat. Ha a hálózat nagy, akkor az élek teljesen véletlenszerű elhelyezése ellenére majdnem minden ponthoz nagyjából azonos számú él fog tartozni.
A jelenség jól szemléltethető úgy, hogy a koktélparti után megkérdezünk minden vendéget, hogy hány ismeretséget kötött. Miután mindenki elment, egy hisztogramot3 rajzolhatunk úgy, hogy ábrázoljuk, hány vendégnek lett egy, kettő vagy pontosan k új ismerőse. Erdős és Rényi véletlen modelljére alkalmazva ennek a hisztogramnak az alakját 1982-ben Erdős egyik tanítványa, Bollobás Béla vezette be és bizonyította egzakt matematikai eszközökkel. Ő ma a memphisi egyetem és az angliai Trinity College professzora. Eredménye azt mutatja meg, hogy a hisztogram Poisson-eloszlást követ, amelynek néhány különleges tulajdonsága e könyvben gyakran felbukkan majd. A Poisson-eloszlásnak van egy kiemelkedő csúcsa, ami azt jelzi, hogy a pontok többségéhez ugyanannyi él csatlakozik, mint az átlagos csúcshoz. Ennek a két oldalán az eloszlás gyorsan csökken, jelezve, hogy az átlagtól való jelentős eltérések különlegesen ritkák.
Vetítsük vissza ezt a hatmilliárd emberből álló társadalomra. Ha igaz a Poisson-eloszlás, akkor a többségünknek nagyjából azonos számú barátja és ismerőse van, és exponenciálisan ritkán találunk olyan embert, akinek az átlagnál lényegesen több vagy kevesebb barátja és ismerőse van. Ezért a véletlen gráfelmélet előrejelzése szerint, ha véletlenszerűen jelöljük ki a szociális kapcsolatokat, akkor egy rendkívül demokratikus társadalomhoz jutunk el, ahol mindegyikünk átlagos, és nagyon kevesen térnek el ettől a nagyon szociális vagy teljesen aszociális típus irányába. Egy nagyon egységes szerkezetű hálózatot kapunk, amelyben az átlagos esetek a leggyakoribbak.
Erdős és Rényi véletlenszerű világegyetemét az átlagok dominálják. A modell szerint a legtöbb embernek nagyjából azonos számú ismerőse van, a legtöbb neuron közel azonos számú másik neuronnal kapcsolódik, a legtöbb vállalat nagyjából azonos számú másik vállalattal kereskedik, a legtöbb weboldalt körülbelül ugyanannyian látogatják. Ahogy a természet vakon dobálja a kapcsolatokat széjjel, hosszú távon egyetlen pont sem lesz kitüntetett vagy kihagyott.
9.
A hálózatokra vonatkozó tudományos gondolkodás 1959-es bevezetése óta meghatározó Erdősnek és Rényinek a véletlen hálózatokról szóló elmélete. Többszörös szemléletváltást hozott, ami tudatosan vagy nem, de bevésődött mindenkinek a gondolkodásába, aki hálózatokkal foglalkozik. Egyenlőségjelet tett a komplexitás és a véletlen közé. Ha egy hálózat túl bonyolult volt ahhoz, hogy egyszerű feltételekkel leírják, akkor ez arra ösztönözte a kutatókat, hogy véletlen hálózatnak tekintsék. Több mint valószínű, hogy a társadalom, egy sejt, a távközlési hálózatok vagy a gazdaság egyaránt eléggé komplex, hogy jól illeszkedjen ebbe a képbe.
De mégis, valami gyanús ezzel a véletlenszerű világegyetemmel, ahol minden pont egyenlő. Meg tudtam volna-e írni ezt a könyvet, ha a testem molekulái úgy döntenek, hogy teljesen véletlenszerűen lépnek egymással reakcióba? Lennének-e nemzetek, államok, iskolák és templomok, vagy bármilyen más, a szociális rendre utaló jelenségek, ha az emberek teljesen véletlen módon működnének egymással együtt? Létezne- e gazdaság, ha a vállalatok vevőiket teljesen véletlenszerűen választanák meg, és eladóikat kockák millióival helyettesítenék? Többségünk úgy érzi, hogy a világ, amelyben élünk, nem véletlenszerű, és hogy a komplex rendszerek mögött valamilyen rendnek kell lennie.
Akkor miért vélekedett úgy két ilyen páratlan elme, mint Erdős és Rényi, hogy a hálózatok kialakulása egy teljesen véletlen folyamat? A válasz egyszerű. Soha nem próbálták megalkotni a hálózatok kialakulásának általános elméletét. A véletlen hálózatok matematikai szépsége sokkal jobban izgatta őket, mint az, hogy képes-e modelljük híven megragadni a bennünket körülvevő természet hálóit. A biztonság kedvéért 1959- es korszakalkotó cikkükben megjegyezték, hogy a gráfok keletkezése felfogható bizonyos kommunikációs hálózatok (vasút-, út- vagy elektromos hálózati rendszerek stb.) kialakulásának nagyon leegyszerűsített modelljeként. A valódi világba történt rövid kiruccanásuk ellenére ezen a területen munkájukat inkább a probléma matematikai mélységeire vonatkozó óriási kíváncsiságuk motiválta, mint a lehetséges alkalmazások.
Erdős lenne az első, aki egyetértene velünk abban, hogy a valódi hálózatoknak kell, hogy legyen szervező elve, amelyik megkülönbözteti őket az általuk 1959-ben bevezetett véletlen hálózatoktól. De az ő számára ez nem lenne érdekes. A véletlenszerűséget feltételezve egy új világra nyitott ablakot, amelynek matematikai szépsége és következetessége a gráfelmélet későbbi munkái mögötti hajtóerőt adta.
Egészen a közelmúltig csak egyetlen módszerünk volt arra, hogy világunkat leírjuk. Így a hálózatmodellezésben a véletlen hálózatok dominálták gondolkodásunkat. Az összetett valódi hálózatokat alapvetően véletlenszerűnek tekintettük.
Erdős tartja a rekordot abban, hogy érdekes problémákat talál ki, és gondoskodik róla, hogy valaki megoldja. Bár soha nem volt annál a néhány ruhánál több tulajdona, mint amennyi belefért egy kis bőr kézitáskába, amellyel mindig utazott, mégis gyakran ajánlott fel az általa érdekesnek talált problémák megoldásáért vagy bizonyításáért pénzjutalmat. Öt dollárt, ha a problémát egyszerűnek gondolta, az igazán nehezekért pedig ötszáz dollárt. És valóban boldogan fizetett, ha a bizonyítást valaki benyújtotta. Nem számított, ha gyakran az egydolláros probléma nehezebbnek bizonyult az ötszáz dollárosnál. A szerencsés matematikusok, akik megkapták a jutalmak egyikét, soha nem vették fel a csekkért járó készpénzt. A csekket többségük bekereteztette. A jutalom a század egyedülálló zsenijétől származó különleges elismerés volt, semmi pénz nem ért volna fel a díj szellemi értékével.
Kövessük Erdős példáját, és tegyünk fel egy kérdést, amit ő soha nem vizsgált. Milyenek a valódi hálózatok? A probléma ilyen pontatlan felvetésével soha nem lett volna elégedett. Ez így túl tág. Lehet, hogy egyértelmű válasz nem is adható rá. Könnyen lehet, hogy soha nem találunk precíz bizonyítást hozzá. Ilyen formában valószínűleg nincs is benne a Könyvben, ami Erdős számára a jó matematikai bizonyítások és tételek gyűjteménye. Lehet, hogy ez a kérdés nem nyerte volna el Erdős tetszését, de a következő fejezetekben meg fogjuk látni, hogy a matematika világán kívül milyen óriási előrelépést jelent.

1985 · Képforrás
